ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2016) Health Science and Bio Convergence Technology: Edition-I
Time difference of arrival based localization for patient monitoring and tracking
The increasing exploitation of wireless sensor devices in Medical diagnostics and patient monitoring has attracted the researchers in the past few decades. Nowadays, the development of health care systems and infrastructure is one of the most demanding and convincing goals. The monitoring and supervision of patients which has been carried out are often executed manually. This paper provides patient monitoring, tracking and localization through wireless sensor networks. We proposed a novel hybrid localization method based on Time Difference of Arrival and Lagrangian multiplier to locate the position of sensor which provides patient localization for Health Care Support. This system performs the localization out of samples of Time Difference of Arrival, tracking and monitoring module based on accelerometer and low pass filter with oversampling algorithm. Also we have designed a hardware setup for monitoring moving target localization and tracking. The simulation results reveal that the proposed method achieved very high localization accuracy.
Keywords
Medical healthcare, Time difference of arrival, Wireless sensor networks, Patient localization.
Introduction
More recently, precise and accurate localization is the most essential science and technology needed for medical applications. Localization in wireless sensor networks has been a long-standing and significant concern that has attracted lots of awareness recently [1]. This work illustrates the design and optimization of a lightweight system based on Wireless Sensor Networks (WSNs) for the habitual supervision of patients which includes the major functionalities of Patient’s status monitoring, Patient localization and tracking. Based on distance measurement numerous efficient methods such as received signal strength indicator (RSSI) [2], time-of-arrival (TOA) [3-4], time-difference-of-arrival (TDOA) [5], and angle-of-arrival (AOA) [6] and etc are being used for location.
However, received signal strength (RSS) accuracy is very less due low signal strength in indoor environment [7]. The methods based on angle-of-arrival (AOA) require highly expensive hardware (antennas) [8]. In time-of-arrival (TOA) localization, the signal travelling time between sending and receiving nodes are measured and used to estimate range. Due to the synchronization error TOA measurements have a positive bias which possibly leads to a huge localization error [9]. Since the synchronization between the source node and the receiving node is not necessary in TDOA method [10] and is not depending on the source transmission time, the best solution for the above problem is using Time Difference-of- Arrival (TDOA) measurements. The travel time of two different signals between a source node and receiver node is measured using TDOA method and this can achieve a high degree of accuracy. The authors in projected decentralized scheme by in-network sensor pairing technique and applied connected dominating set (CDS) to attain TDOA measurement [11]. However, this scheme requires less energy consumption, network bandwidth and communication cost. The author proposed Positive semi definite programming and the use of Gaussian distribution for squared error of the measured distance to convert non-convex optimization into convex function [12]. In [13], the author presented TOA measurement in asynchronous networks, which produces a very high localization error because of synchronization error. However to reduce the localization error they used TDOA measurement and estimate source transmit time in addition to the source location. Also, they proposed a novel semi definite programming by translating non-convex maximum likelihood estimator into a convex optimization. To relax the approximate maximum likelihood estimation problem in line-of-sight and non-line-of-sight atmosphere a relaxation technique of semi definite programming (SDP) for ultra wide band WSNs was proposed [14].
To obtain an accurate location of moving target Lee et al. [15] proposed hybrid trilateration algorithm based on EKF. They employed several sensors and estimate the position using time synchronization and velocity of target. To reimburse the trajectory error with respect to time and distance, the self localization facility is necessary in the autonomous navigation of an indoor moving target. The EKF algorithm with the global ultrasonic system is used for this localization [16]. The authors [17-18] used mixed supervised and unsupervised time series analysis methods and uses accelerometers to recognize the location of sensors on human body and guarantee the accuracy of measurements in health and medical observing systems. There are considerable raise in the number of an assortment of health monitoring devices. Conventionally, personal medical monitoring systems have been used to collect the information. Usually, systems with numerous sensors for substantial therapy attribute bulky wires between the sensors and the monitoring system. These huge wires may bound the patient's movement and thus the measured results may be negative [19].
Modern technology progress an integration of sensors have facilitate a new invention of wireless sensor networks appropriate for many applications like health monitoring and supervision, habitat monitoring [20], traffic pattern monitoring and steering, plant monitoring in agriculture [21], and infrastructure monitoring. Medical applications are a growing field with vast intact applications like drug delivery, or the development of mobile treatment systems. Localization in WSNs have a wide range of medical applications such as the habitual and remote monitoring and tracking of patients, Medical and Surgical, Personal Assistance, Security/ Surveillance, Warehouse and Distribution Accessibility- Inspection of sites inaccessible to humans, Manufacturing plants, etc. [22,23].
M. D’Souza et al. presented an indoor environment wireless localization network for patients tracking. They set some fixed nodes all around the building in a grid fashion and at any time the mobile node are detected using at least three fixed nodes. The position of the node is estimated through triangle’s centroid method and the frequency of beacons is transported to the central controller which is sent by mobile node. The localization accuracy is related with the number of fixed nodes [24].
In previous work the system performs localization using samples of RSSI algorithm [25]. The main drawback of RSSI is low signal strength at indoor environment. So we proposed a novel hybrid technique to improve the performance of the existing methods in TDOA with Lagrangian multiplier. The foremost objective of relaxation technique gives the better accuracy and improves the convergence rate dramatically. Also we have designed one hardware setup for monitoring the target localization and tracking through wireless sensor networks using the TDOA measurement.
The residue of the paper is structured as follows: Section 2 describes the system design using Time Difference-of-Arrival (TDOA) localization. In section 3 the network architecture of Patient Localization and Tracking system are presented. Section 4 reports the performance evaluation for TDOA system and Mobile Target Localization through simulation. Concluding observations are given in section [5].
TDOA system design
The measurement model TDOA localization is labeled in this section. Consider a Wireless Sensor Networks, which consists of a huge number of k sensor nodes with coordinates (xk,yk) (1≤ k ≤ n) and a lesser amount of i anchor nodes with coordinates (xi,yi) (1≤ i ≤ n) deployed in two dimensional geographical area [0,D] *[0,D].Each node having a communication range ‘R’ which should be less than zero (i.e., R<0).Throughout the localization progression, every receiving sensor identifies the time of arrival of the signal from the source sensor. The measured Time Difference of Arrival between nth anchor node and mth anchor node is demonstrated as
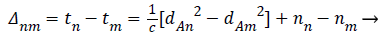 (1)
(1)
Where, Δnm be the Time Difference of Arrival measurement. The speed of light or the propagation velocity of the signal c is dependent on the environment where the network is to be deployed (e.g., for free space the propagation velocity is c 3 × 108 m/s).
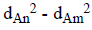 is the actual distance of two sending and receiving
sensors
is the actual distance of two sending and receiving
sensors
nn–nm is the TDOA noise (estimation error).
In Time measurement, the source localization problem can be rectified by the least square estimator which is given by
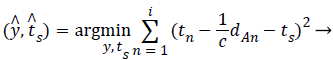 (2)
(2)
ts be the source transmit time which is unknown and to be measured
This LS estimator is a nonlinear non-convex problem. So we need to convert this nonlinear non-convex problem into convex ones. To tackle this problem the maximum likelihood estimator is attained.
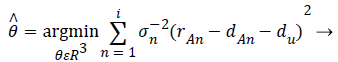 (3)
(3)
So the optimization problem of maximum likelihood estimator can be transcribed as
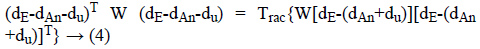
Now we define the new vector
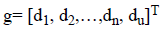
then we can write
dAn+du=Vg → (5)
Where V=[IN,0N], and
IN and 0N denote the N × N Identity and Zero matrices
Persevering (8) and (9) produces
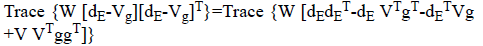
Trace 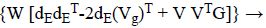 (6)
(6)
Where G=ggT
The G matrix diagonal elements are given by
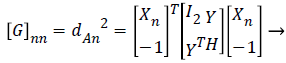 (7)
(7)
Where H=YTY. To convert a non-convex optimization into a convex cost function, relax the matrix G and the variable H. Using the Schur complement the G matrix and the variable H can be written as a function of Linear Matrix Inequality (LMI).
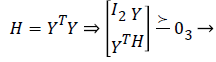 (8)
(8)
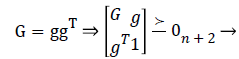 (9)
(9)
As a result, the nonlinear- nonconvex cost function of the maximum likelihood estimator problem is relaxed into semidefinite programming optimization method that will result in Lagrangian problem.
So, we proposed a novel SDP- Multiplier TDOA method. The major role of the multiplier is to derive Lagrangian problem towards a solution that satisfies the relaxed constraints. Using this reformulation of optimization problems, adding Lagrangian multiplier (λ) in the objective function gives the minimum value of the function and improves the convergence rate dramatically.
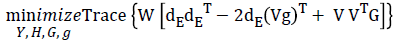
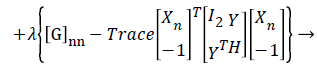 (10)
(10)
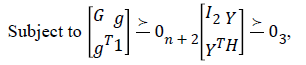
The above equation is used to find the estimated position of sensor nodes. The localization error is calculated as the distance between the actual distance and the estimated distance.
System Model for Patient Localization and Tracking
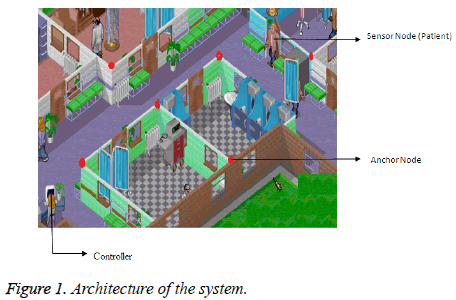
Network architecture: The network system architecture is composed of three modules: (i) establish the anchor nodes, which are statically deployed in the areas to be supervised; (ii) sensor nodes, which are attached to patients for localization and tracking services. iii) Build a controller. The architecture of the system is shown in figure 1.Also to monitor the body movement and postural orientation of patient accelerometer is used.
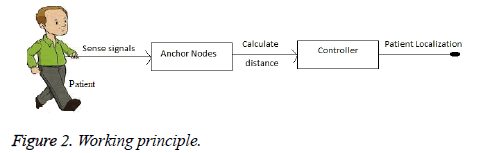
The working principle is as follows: i) when the patient enters in the areas to be supervised the anchor nodes monitor and sense the signal of the patient by multihop communication. ii) Calculate the distance using Time Difference of Arrival localization algorithm. Then all the information is passed to the controller. The controller will easily find the exact position of the patient.
The experimental hardware setup for tracking the moving target (i.e., patient) shown in Figure 3. In this experiment we have used 4 anchor nodes in an IC LM358 sensor board. When the moving target enters in the particular area, the nearby anchor node senses the target signal and calculates the distance. All the information is send to the system/controller which displays the position of the target. Also to increase the tracking performance, we use the error distance. The accuracy of the tracking performance is measured by the mean and standard deviation of error distance.
To improve the localization accuracy and computational complexity oversampling method with Low Pass Filter is used to smooth down the discrepancy of the TDOA samples which are used for error reduction in measurements and to provide accurate localization of posture and orientation. Oversampling algorithm helps with repeated iterations in order to arrive at the accurate outputs. So the probability of locating the target is found to be high accuracy. It samples and groups the output based on their ranges for accuracy and filtering the unwanted noise. Here the computed values are found to be based on the previous position of the target and not on the theoretical values. So the computational complexity is found to be reduced to a great level.
The Algorithm based on oversampling method is given as follows:
• Place the target on the working field
• Locates the exact position (P) by distance calculated
• If Measurement calculated based on distance by ultrasonic sensors.
• Then, target position-(P)
• else
• Locate the target with reference to the previous position
• Now, target position-(P Ref)
• End if
Hence, this oversampling algorithm can then determine the target pose accurately. Efficiency can be expressed by using the moving of target in the rotating of angle in degrees.
Mobile Target Localization
Table.1 gives the trajectories values of the proposed system.
| .Trajectory | Ep (m) | EØ (deg.) | ES (m) |
|---|---|---|---|
| 1 | 0.15 | 1.15 | 0.32 |
| 2 | 0.13 | 1.26 | 0.09 |
| 3 | 0.13 | 2.65 | 0.87 |
| 4 | 0.25 | 3.25 | 0.54 |
Table 1. Trajectory results.
The moving target position E p (m) based on the oversampling algorithm with the application of the low pass filter is given by
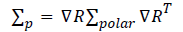
Where Σp – Summation of the position vector,
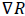 – Effective resistance ratio,
– Effective resistance ratio,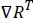 Effective resistance ration
over time.
Effective resistance ration
over time.
The moving target orientation EØ (deg.) is given by
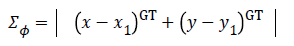
Where Σφ - Summation of Orientation values, GT- Ground Truth
x – Reference position in x-axis, x1 – Position of target at 1st instance
y – Reference position in y-axis, y1 – Position of target at 1st instance
The moving target specification ES (m) of is given by
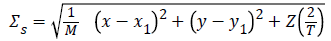
Where Σs – Summation of specified positions,
M – Number of significant points, Z – Root mean square value of the positions, T – Time constant
Localization error
Table 2 shows that the actual position and the measured position of the target and the localization error which is computed by the difference between the actual position and the measured position.
| Actual Position (cm) | Actual Position (cm) | Measured Position (cm) | Measured Position (cm) | Localization Errors (cm) | Localization Errors (cm) |
|---|---|---|---|---|---|
| X | Y | X | Y | X | Y |
| 762 | 360 | 760 | 355 | 2 | 5 |
| 782 | 372 | 783 | 368 | -1 | 4 |
| 820 | 375 | 820 | 376 | 0 | -1 |
| 850 | 410 | 847 | 413 | 3 | -3 |
| 890 | 450 | 891 | 446 | -1 | 4 |
| 920 | 485 | 922 | 484 | -2 | 1 |
Table 2. Localization error.
Performance evaluation
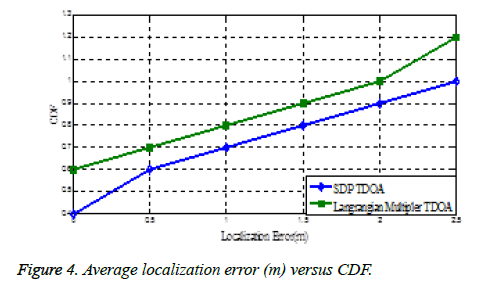
TDOA system: We randomly deployed several anchor nodes at two dimensional square areas of 100 m X 100 m in Non- Line of sight indoor environment at different positions. We consider 3, 6, 9, 12, 15 anchor nodes resulting in densities of 0.03, 0.06, 0.09, 0.12, 0.15 anchors/m2. Figure 4 shows that the average localization error versus Cumulative Distribution Function (CDF). We have evaluated the localization error and the average localization error is found to be 0.925m which is much lesser than the existing works [14].
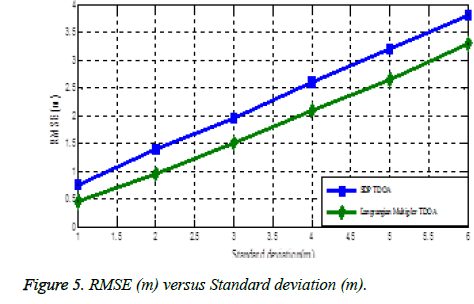
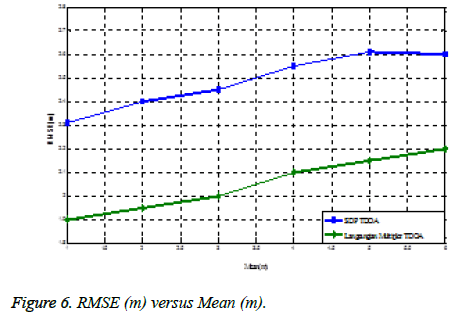
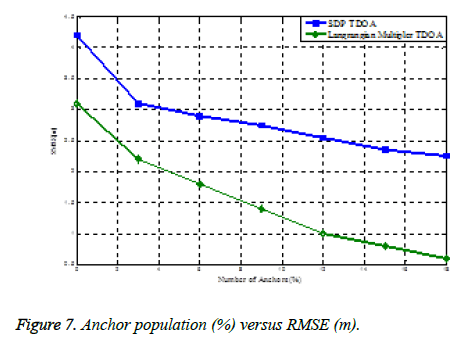
We estimate the RMSE of the source position against different strength of noise standard deviation in NLOS environment. Idyllically, we consider NLOS error is distributed exponentially and distribution parameters are perfectly known. We set the probabilities to be 0.7 and the mean of NLOS error μ is 4m.We carry out the simulation for different values of standard deviation σn. Figure 5 Plots the graph for RMSE versus standard deviation σn. From the figure we realize that the Lagrangian Multiplier TDOA technique has achieved good position estimation in the NLOS environment which has less localization errors. We set the standard deviation σn is 4m.We have simulated for different mean values of NLOS error μ. Plot the graph for RMSE versus a mean of NLOS error μ which is shown in Figure 6. From the figure we recognize that the localization accuracy of the proposed Lagrangian-Multiplier TDOA technique has succeeded for the NLOS environment by diminishing the localization errors. We have varied anchor population for 3%, 6%, 9%, 12%, 15%,… and plotted the graph for RMSE values which is shown in Figure 7.The figure proves that the good organization of our proposed method has reduced the localization errors in NLOS environments.
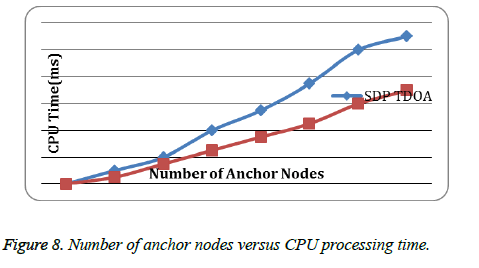
Moreover the localization processing time is also a vital concern. To attain suitable localization accuracy the system should have the low processing time. The processing time based on TDOA with lagrangian multiplier is less which is shown in Figure 8.
Trajectory response of moving target
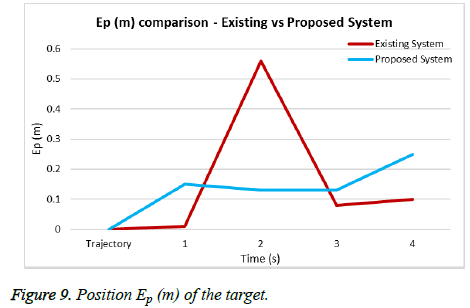
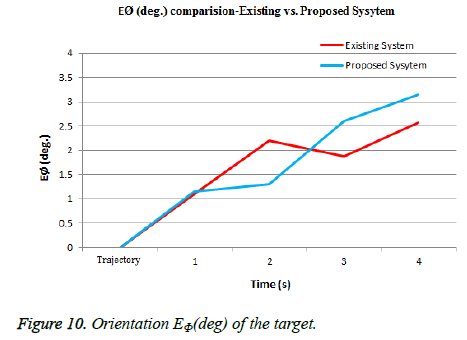
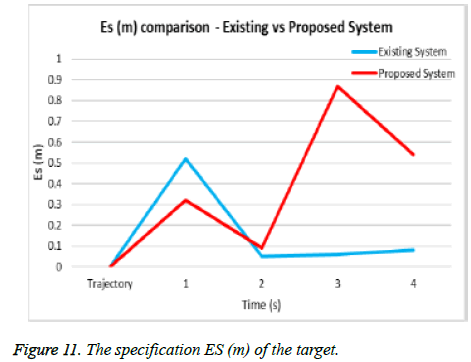
We evaluate the performance of the moving target using oversampling method with Low Pass Filter. The target is tracked when moving along a prefixed trail in an indoor environment. The trail is sampled for Lagrangian multiplier TDOA message response with ground truth position of the moving target. At each Lagrangian multiplier TDOA packet the position of the moving target is calculated. The Figure 9 gives the output with respect to the position Ep (m) of the target in comparison with the existing system [26]. The accuracy is obtained with good performance and less computational complexity. The orientation of the target EØ (deg) is done based on the values that are returned from the sensors shown in figure10. The values obtained are used for the orientation of the target estimation. The specification of motion of the target ES (m) is shown in Figure 11. The accuracy is high as the destination reached is clearly notified.
Conclusion
The development of health care systems and infrastructure is one of the most demanding and convincing goals in recent days. The monitoring and supervision of patients which has been carried out are often executed manually. This paper provides patient monitoring, tracking and localization through wireless sensor networks. We proposed a novel hybrid localization method based on Time Difference of Arrival and Lagrangian multiplier to locate the position of sensor. We randomly deployed several anchor nodes in Non-Line Of Sight indoor environment at different positions. We have evaluated the localization error and the average localization error is found to be 0.925m which is much lesser than the existing works. Also we have designed a hardware setup for monitoring moving target localization and tracking. Oversampling method with Low Pass Filter is used to increase the accuracy. The simulation results reveal that the proposed method achieved very high localization accuracy.
References
- Pahlavan K, Krishnamurth P, Geng V. Localization challenges for the Emergence of the Smart World. IEEE Access2015.
- PaulS,WanEA. RSSI-based Indoor Localization and tracking using Sigma point Kalman smoothers. IEEE JSignal Process 2009; 3: 860-873.
- Xu E, Ding Z, Dasgupta S. Source localization in wireless sensor networks from signal time-of-arrival measurements. IEEE Transact Signal Process 2011.
- Shen J,Molish AF, Salmi J. Accurate Passive Location estimation using TOA Measurements. IEEE Transact Wireless Commun 2012.
- Meng W, Xie L, Xiao W. Decentralized TDOA Sensor Pairing in Multihop Wireless Sensor Networks. IEEE Signal Process Lett 2013.
- Zhu Y, Huang D, Jiang A. Network localization using angle of arrival. Proc IEEE Int Confer Electro/Informa Technol 2008.
- Zàruba GV. Indoor location tracking using RSSI readings from a single Wi-Fi access point. Wireless Networks2007.
- Andersen JB, Pedersen KI. Angle-of-arrival statistics for low resolution antennas. IEEE Transact Antennas Propagat2002.
- Li X, Pahlavan K. Super-Resolution TOA Estimation With Diversity for Indoor Geolocation. IEEE Transact Wireless Commun 2044; 3: 224-234.
- Zheng J, Wu YC. Localization and Time Synchronization in Wireless Sensor Networks: A Unified Approach 2008 IEEE Asia Pacific Conference on Circuits and Systems, Macao, 2008.
- Meng W, Xie L, Xiao W. Decentralized TDOA Sensor Pairing in Multihop Wireless Sensor Networks. IEEE Signal Process Lett 2013.
- Xie S, Wang J, Hu A, Gu Y, Xu J. Positive Semi-definite Programming Localization in Wireless Sensor Networks, 2015.
- Vaghefi RM, Buehrer RM. Asynchronous Time-of-Arrival-Based Source Localization. Proceed IEEE Int Confer AcousticsSpeech Signal Process2013.
- Chen H, Kenneth W, Lui K, Wang Z, So HC, Poor HV. Non-line-of-sight Node Localization based on Semi-Definite Programming in Wireless Sensor Networks. 2009.
- Lee KW, Park JB, Lee BH. Dynamic localization with hybrid trilateration for mobile robots in intelligent space.Intell Service Robotics2008.
- Yi SY, Choi BW. Autonomous navigation of indoor mobile robots using a global ultrasonic system.Robotica2004; 22: 369-374.
- Vahdatpour A, Amini N, Xu W, Sarrafzadeh M. Accelerometer-based on body sensor localization for health and medical monitoring applications. Pervasive Mob Comput 2011; 7: 746-760.
- Vahdatpour A, Sarrafzadeh M. Unsupervised discovery of abnormal activity occurrences in multidimensional time series, with applications in wearable systems. SDM ’10: Siam Conference on Data Mining. 2010.
- Martin T, Jovanov E, Raskovic D. Issues in Wearable Computing for Medical Monitoring Applications: A Case Study of a Wearable ECG Monitoring Device. International Symposium on Wearable Computers ISWC 2000, Atlanta, 2000.
- Szewczyk R, Osterweil E, Polastre J, Hamilton M, Mainwaring A, Estrin D. Habitat monitoring with sensor networks. Commun ACM 2044; 47: 34-40.
- Burrell J, Brooke T, Beckwith R. Vineyard Computing: Sensor Networks in Agricultural. IEEE Pervasive Comput 2004; 3: 38-45.
- Jovanov E, Price J, Raskovic D, Kavi K, Martin T, Adhami R. Wireless Personal Area Networks in Telemedical Environment. in Proceedings of the Third International Conference on Information technology in Biomedicine (ITAB-ITIS2000), Arlington, VA, 2000.
- Jovanov E, Lords A, Raskovic D, Cox P, Adhami R, Andrasik F. Stress Monitoring Using a Distributed Wireless Intelligent Sensor System. IEEE Eng Med Biol Magazine 2003; 22: 49-55.
- D’Souza M, Wark T, Ros M. Wireless localization network for patient tracking. 2008.
- Alessandro R. An integrated system based on wireless sensor networks for patient monitoring, localization and tracking.Ad Hoc Networks11.1 2013.
- Kim SJ, Kim BK. Dynamic Ultrasonic Hybrid Localization System for Indoor Mobile Robots. IEEE Transact Indust Electron 2013.