ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2018) Volume 29, Issue 7
The use of several information criteria for logistic regression model to investigate the effects of diabetic drugs on HbA1c levels
1Faculty of Engineering, Department of Industrial Engineering, Ondokuz Mayis University, Samsun, Turkey
2Faculty of Science and Letters, Department of Statistics, Ondokuz Mayis University, Samsun, Turkey
3Faculty of Medicine, Department of Histology and Embryology, Ondokuz Mayis University, Samsun, Turkey
- *Corresponding Author:
- Mehmet Emin Onger
Faculty of Medicine
Department of Histology and Embryology
Ondokuz Mayis University, Samsun, Turkey
Accepted on January 23, 2018
DOI: 10.4066/biomedicalresearch.29-17-2871
Visit for more related articles at Biomedical ResearchHbA1c measurement is an important indicator for checking the diabetes care in a patient. There are several drugs to hold HbA1c in desired level. Diabetic drugs assist the patients for decreasing the glucose level so HbA1c level can be healed. In this article we investigated the effects of diabetic drugs on HbA1c level for type 2 diabetes patients. We implemented variable selection procedures with logistic regression analysis. Particle Swarm Optimization (PSO) was used to minimize the fitness function of the regarding models with several information criteria. According to selection system of the information criteria, we obtained different variable subsets and interpreted the regression models. In application part, we evaluated each selected logistic regression model and identified the common efficient drugs for HbA1c level. Our results demonstrate that Insulin, Metformin, Glyburide, Glipizide and Glimepiride are the joint effective drugs. Also Insulin is the most influential drug to balance the HbA1c level of diabetic patients.
Keywords
Diabetic drugs, Variable selection, Information criteria.
Introduction
Type 2 diabetes is one of the most serious medical conditions faced by today’s word. The number of people with Type 2 diabetes has increased enormously. It can causes serious health problems if it can’t be kept under control. HbA1c, which measures glucose levels chemically bound to hemoglobin, is an important indicator for checking the diabetes care in a patient. Over time, high blood sugar levels causes more glucose to bind with hemoglobin, so a high HbA1c percentage indicates that blood sugar levels are high on average. Many experts believe that an HbA1c level below 7 percent is associated with a lower risk of diabetes complications, such as kidney disease and eye disease that can lead to blindness. Therefore it must be kept below 7 percent. There are several drugs to hold HbA1c in desired level. Diabetic drugs assist the patients for decreasing the glucose level to keep the HbA1c low.
The last two decades have witnessed that many new pharmacotherapy options have become available. Currently there are 11 classes of diabetes medications, including sulfonylureas, meglitinides, Glucagon-Like Peptide-1 (GLP-1) receptor agonists, biguanides, an amylin analogue, thiazolidinediones, bromocriptine, alpha-glucosidase inhibitors, Dipeptidyl Peptidase-4 (DPP-4) inhibitors, colesevalam (a bile-acid sequestrant), and insulin [1,2]. Many studies have been performed pairwise comparisons for the effectiveness of medicines about HbA1c. From those studies it can be summarized that most medications reduced HbA1c in a similar way [3-6].
While pairwise comparisons for the effectiveness of medicines about HbA1c are well studied, little is studied on the effectiveness of all medicines about HbA1c in a regression approach.
This study focuses on identifying of the common efficient drugs for HbA1c using logistic regression model for model selection. As an optimization tool, Particle Swarm Optimization (PSO) is selected to minimize the fitness function of the regarding models with several information criteria.
PSO has strong properties to optimize the fitness functions because it benefits the heuristic searching strategy. The information criteria are the fitness functions of the logistic regression models.
These criteria are minimized with PSO algorithm. In this study, according to selection system of the information criteria, different variable subsets are obtained and the regression models are interpreted.
For application, we evaluate each selected logistic regression model and identify the common efficient drugs for HbA1c level.
Materials and Methods
Binary logistic regression analysis
Logistic regression analysis is a commonly used technique in classification tasks. Type of the logistic regression analysis varies with the number of categories of response variable. When the response variable has two categories, binary logistic regression is implemented. In practice, there are several link functions that used for dichotomous response in logistic regression such as logit, probit, complementary log-log and log-log functions [7]. Generally logit transformation is employed and the formula for logit link is: p=1/(1+exp(- Xβ))-----(1)
Where μ=Xβ, X=(X1, X2,…., X3) is the vector of predictors and β=(β1, β2,…, βp) is vector of regression coefficients. Regression coefficients are estimated with the maximization of the log-likelihood function of the binary logistic regression model. Log-likelihood function of the model is:
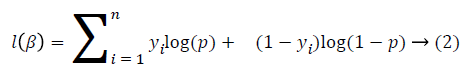
General approach for optimizing this function is to use Newton-Raphson algorithm [8]. After obtaining the regression coefficients, the interpretation becomes possible by applying exponential transformation on beta coefficients.
Information criteria for logistic regression models
Information criteria are used to represent the quality of the models. Especially, information criteria are very important during variable selection process. Selected models are highly related to the used information criteria in regression modelling. The proper selection of the information criteria leads the determination of true independent factors which affect the dependent variable. In regression analysis, the main aim is to select a predictor set that minimizes information criteria value.
All information criteria are based on penalizing the regression models. There are three components to penalize the models: number of variables, observations and complexity of the covariance matrix of the regression coefficients. These components can vary according to structure of the information criteria.
For the variable selection task, five information criteria are considered. These are Akaike Information Criteria (AIC), corrected Akaike Information Criteria (AICc), Bayesian Information Criteria (BIC) and Information Complexity type Criteria (ICOMP) [9-14]. The formulations of the information criteria are as the following:
AIC=-2 log L (M̂ )+2k → (3)
AICc=-2 log L (M̂ )+2k (k+1)/(n-k-1) → (4)
BIC=-2logL (M̂ )+klog (n) → (5)
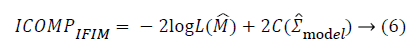
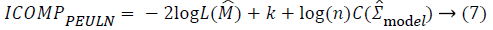
In these equations, “n” shows sample size, k shows the number
of variables and  shows the complexity of the
covariance matrix of parameters. It is seen from the
formulations that AIC is based on only penalizing the number
of variables in the model. AICc is a modified version of
classical AIC and it take the sample size into consideration.
BIC also considers number of variables and observations
similar to AICc but the penalization differs. Unlike other
criteria, ICOMP type criteria penalize the complexity of the
regression coefficients via covariance matrix. The penalization
of the covariance matrix of the coefficients is performed with a
complexity function C (.) defined as:
shows the complexity of the
covariance matrix of parameters. It is seen from the
formulations that AIC is based on only penalizing the number
of variables in the model. AICc is a modified version of
classical AIC and it take the sample size into consideration.
BIC also considers number of variables and observations
similar to AICc but the penalization differs. Unlike other
criteria, ICOMP type criteria penalize the complexity of the
regression coefficients via covariance matrix. The penalization
of the covariance matrix of the coefficients is performed with a
complexity function C (.) defined as:
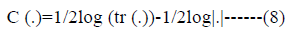
We utilized five information criteria to choose relevant determinants for Hba1c levels by using heuristic optimization. PSO algorithm was employed to minimize information criteria value with assigning 0-1 values to each predictors and selected the optimal variable set. All the information criteria were evaluated in binary logistic regression analysis.
Discrete PSO for variable selection
PSO is a heuristic optimization technique which is based on swarm intelligence [15]. This optimization method is inspired from the movements of bird flocks. PSO employs through the simulations of birth flocking [16]. Bird flocking tries to optimize the fitness function via agents. The agents update their positions according to their best values that achieved so far which are called as “pbest”. Also the agents have information about their best values among other population members and this information is called as “gbest”. The positions of the agents are changed using pbest, gbest and velocities. The velocities are arranged as the following formulation:
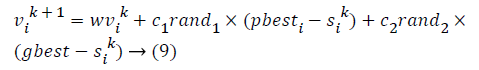
In equation (1) “i” indicates the agent and “k” indicates the iteration. ѵi is the velocity and Si k is the current position of agent. rand is a random real number between 0-1. c1 and c2 are the weighting coefficients and “w” represents the weighting function. This function is shown as:
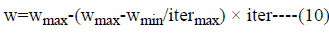
In equation (2), wmax is the initial and wmin is the final weight. “iter” shows the iteration number and itermax shows the maximum number of iteration. The agent’s struggles to find positions that converge for pbest and gbest. The position of the agents are updated with
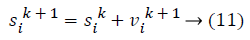
To perform the variable selection task with PSO, a discrete transformation is required for the velocity. The transformation is as the following:
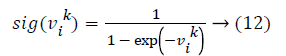
Where sig (.) is the sigmoid function. In variable selection problem the solution sets are considered as binary vectors. These vectors contain 0-1 integer values which 0 indicates exclusion and 1 inclusion of the regarding variable. Solution vector is represented as binary coded vector for p explanatory variables as follows:
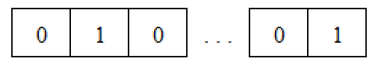
X1 X2 X3 Xp-1 XP
According to solution set, PSO algorithm employs to minimize the objective function of the logistic regression model. Objective functions are selected as the information criteria of the model.
Results
In application part we investigated the effects of the drugs on HbA1c. The used dataset was imported from UCI Machine learning repository [17,18]. All variables were transformed to binary for the suitability of the implementation. Dependent variable was considered as the HbA1c levels. The threshold value was chosen as 7% similar to previous studies [8]. These levels were grouped in two categories such as normal and nonnormal depending on the threshold value. If the HbA1c level was higher than 7%, dependent variable was labelled as normal; in opposite cases it was labelled as normal. Explanatory variables were taken as the diabetic drugs. According to usage of the drug, we assigned 0-1 values to each observation. In this dataset “0” means that the patient does not use the drug and “1” means that the patient regularly uses the drug. With the mentioned transformations, the dataset becomes suitable to implement binary logistic regression analysis. This study is limited for the diabetes patients whose HbA1c values are normal and non-normal. Because of this limitation, there is no discrimination for the early and late diabetes patients.
To assess the effects of the diabetic drugs, we used sixteen different type drugs as the independent variables. The names of the diabetic drugs are Metformin, Repaglinide, Nateglinide, Chlorpropamide, Glimepiride, Glipizide, Glyburid, Tolbutami, Pioglitazone, Rosiglitazone, Acarbose, Miglitol, Tolazamide, Insulin, Glyburide-metformin, Glipizid metformin, respectively. The recent studies showed the achievement of the mentioned diabetic drugs.
We performed variable selection within the binary logistic regression based on PSO optimization. The main task of application study is to minimize the information criteria value of the logistic regression model using PSO algorithm. This analysis enables to see which drugs are effective on HbA1c levels from the perspectives of information criteria. The applications were completed with R programming language. PSO algorithm was implemented with PSO package which exists in R [19]. Variable selection was employed within several information criteria. These information criteria are AIC, AICc, BIC, ICOMPIFIM and ICOMPPEULN. Each information criteria determined different subsets of drugs.
We reported the statistics for each logistic regression models that obtained with variable selection process from Tables 1-5. The model statistics consist of regression coefficient estimates, standard errors, z-values and significance values for each explanatory factor. In these results, the negative regression coefficients represent the decrement of the HbA1c level for the relevant drug. All the drugs have healing effects due to the reduction of HbA1c levels on the basis of selected models instead of Nateglinide. The use of Nateglinide does not decrease the HbA1c level. The effects of the drugs are sorted with the z-values of regression coefficients. Insulin is the most effective drug for all selected models because the absolute zvalue is the highest among other drugs. Determinative factor on these results is information criteria so the results vary according to information criteria. From the above results, we can observe that AIC type criteria and ICOMPIFIM select more variables AICc selects the full variable sets so there may be an over fitting problem. BIC and ICOMPPEULN select more parsimonious models. In the models that selected with AIC, AICc and ICOMPIFIM, Nateglinide and Pioglitazone have positive effects on HbA1c so these three criteria cause misleading results. Other information criteria are consistent and all regression coefficients are negative. For all the selected models, many of the predictors have statistically significant effects on HbA1c levels so these models are available for the inference.
| Coefficient | Estimate | Standard error | Z value | Sig. |
|---|---|---|---|---|
| (Intercept) | -0.367 | 0.039 | -9.472 | <0.001 |
| Metformin | -0.271 | 0.059 | -4.605 | <0.001 |
| Repaglinide | -0.261 | 0.183 | -1.425 | 0.154 |
| Nateglinide | 0.754 | 0.324 | 2.325 | 0.02 |
| Glimepiride | -0.496 | 0.113 | -4.371 | <0.001 |
| Glipizide | -0.345 | 0.072 | -4.802 | <0.001 |
| Glyburide | -0.475 | 0.076 | -6.229 | <0.001 |
| Miglitol | -11.4 | 155.214 | -0.073 | 0.942 |
| Insulin | -0.792 | 0.046 | -17.05 | <0.001 |
Table 1. Model statistics based on the selected predictors with AIC.
| Coefficient | Estimate | Standard error | Z value | Sig. |
|---|---|---|---|---|
| (Intercept) | -0.359 | 0.039 | -9.14 | <0.001 |
| Metformin | -0.267 | 0.059 | -4.507 | <0.001 |
| Repaglinide | -0.259 | 0.183 | -1.414 | 0.158 |
| Nateglinide | 0.745 | 0.325 | 2.294 | 0.022 |
| Chlorpropamide | -0.208 | 0.713 | -0.291 | 0.771 |
| Glimepiride | -0.494 | 0.114 | -4.34 | <0.001 |
| Glipizide | -0.343 | 0.072 | -4.756 | <0.001 |
| Glyburide | -0.473 | 0.076 | -6.188 | <0.001 |
| Tolbutamide | -11.578 | 228.597 | -0.051 | 0.96 |
| Pioglitazone | 0.032 | 0.094 | 0.341 | 0.733 |
| Rosiglitazone | -0.096 | 0.09 | -1.07 | 0.285 |
| Acarbose | -0.298 | 0.465 | -0.64 | 0.522 |
| Miglitol | -11.358 | 153.385 | -0.074 | 0.941 |
| Tolazamide | -1.132 | 1.1 | -1.029 | 0.303 |
| Insulin | -0.794 | 0.047 | -17.062 | <0.001 |
| Glyburide- metformin | -0.222 | 0.325 | -0.685 | 0.493 |
| Glipizide-metformin | -12.207 | 324.744 | -0.038 | 0.97 |
Table 2. Model statistics based on the selected predictors with AICc.
| Coefficient | Estimate | Standard error | Z value | Sig. |
|---|---|---|---|---|
| (Intercept) | -0.368 | 0.039 | -9.534 | <0.001 |
| Metformin | -0.271 | 0.059 | -4.613 | <0.001 |
| Glimepiride | -0.496 | 0.113 | -4.371 | <0.001 |
| Glipizide | -0.345 | 0.072 | -4.803 | <0.001 |
| Glyburide | -0.477 | 0.076 | -6.262 | <0.001 |
| Insulin | -0.792 | 0.046 | -17.062 | <0.001 |
Table 3. Model statistics based on the selected predictors with BIC.
| Coefficient | Estimate | Standard error | Z value | Sig. |
|---|---|---|---|---|
| (Intercept) | -0.369 | 0.039 | -9.566 | <0.001 |
| Metformin | -0.273 | 0.059 | -4.637 | <0.001 |
| Nateglinide | 0.752 | 0.325 | 2.317 | 0.021 |
| Glimepiride | -0.495 | 0.113 | -4.363 | <0.001 |
| Glipizide | -0.344 | 0.072 | -4.792 | <0.001 |
| Glyburide | -0.471 | 0.076 | -6.179 | <0.001 |
| Tolbutamide | -11.568 | 228.58 | -0.051 | 0.96 |
| Miglitol | -11.396 | 155.202 | -0.073 | 0.942 |
| Insulin | -0.795 | 0.046 | -17.108 | <0.001 |
| Glipizide-metformin | -12.197 | 324.744 | -0.038 | 0.97 |
Table 4. Model statistics based on the selected predictors with ICOMPIFIM
| Coefficient | Estimate | Standard error | Z value | Sig. |
|---|---|---|---|---|
| (Intercept) | -0.363 | 0.039 | -9.366 | <0.001 |
| Metformin | -0.264 | 0.059 | -4.468 | <0.001 |
| Glimepiride | -0.491 | 0.113 | -4.324 | <0.001 |
| Glipizide | -0.34 | 0.072 | -4.727 | <0.001 |
| Glyburide | -0.474 | 0.076 | -6.213 | <0.001 |
| Rosiglitazone | -0.105 | 0.09 | -1.17 | 0.242 |
| Insulin | -0.791 | 0.046 | -17.04 | <0.001 |
Table 5. Model statistics based on the selected predictors with ICOMPPEULN.
Table 6 shows the drugs selected with variable selection produce for each information criteria. We coded the selected drugs with 1 and unselected with 0. The codes with asterisk show the non-significance of the regarding drug. From Table 6, we can identify the drug sets which were included in logistic regression models. According to these results Insulin, Metformin, Glyburide, Glipizide and Glimepiride were jointly selected and these drugs are effective on HbA1c levels. When looking at the parameter estimates in model statistics, insulin has the highest effect on HbA1c levels because the Z value is the highest one in all models. Glimepiride has relatively lower effect on HbA1c levels among the common effective drugs.
| Diabetic drug | AIC | AICc | BIC | ICOMPIFIM | ICOMPPEULN |
|---|---|---|---|---|---|
| Metformin | 1 | 1 | 1 | 1 | 1 |
| Repaglinide | 1* | 1* | 0 | 0 | 0 |
| Nateglinide | 1 | 1 | 0 | 1 | 0 |
| Chlorpropamide | 0 | 1* | 0 | 0 | 0 |
| Glimepiride | 1 | 1 | 1 | 1 | 1 |
| Glipizide | 1 | 1 | 1 | 1 | 1 |
| Glyburide | 1 | 1 | 1 | 1 | 1 |
| Tolbutamide | 0 | 1* | 0 | 1* | 0 |
| Pioglitazone | 0 | 1* | 0 | 0 | 0 |
| Rosiglitazone | 0 | 1* | 0 | 0 | 1* |
| Acarbose | 0 | 1* | 0 | 0 | 0 |
| Miglitol | 1* | 1* | 0 | 1* | 0 |
| Tolazamide | 0 | 1* | 0 | 0 | 0 |
| Insulin | 1 | 1 | 1 | 1 | 1 |
| Glyburide-metformin | 0 | 1* | 0 | 0 | 0 |
| Glipizide-metformin | 0 | 1* | 0 | 1* | 0 |
Table 6. Selected drugs for each information criteria.
In terms of classification accuracy, we evaluated the true classification accuracy ratios. All the information criteria produce the same value, 72.95%. BIC and ICOMP-type criteria have relatively fewer parameters so these models are more eligible by the means of Occam’s Razor principle.
Discussion
Diabetes mellitus has become a broad problem because of the possible dangers on human health. To observe the progress of this disease, HbA1c is an informative measurement. Diabetic drugs provide the patients for regularizing glucose level. In this paper, we present a different way of examining the determinants of HbA1c using variable selection techniques. We benefited the power of PSO algorithm and information criteria with logistic regression analysis. Several information criteria identified distinct models. According to these models, we can make some inferences for diabetes treatment.
Within variable selection framework, we obtained the optimal diabetic drugs and sorted their effects. Our empirical results indicate that the usage of Insulin, Metformin, Glyburide, Glipizide and Glimepiride may mostly aid while struggling with diabetes. Insulin is the most powerful treatment type for regularizing the HbA1c level and it is the best for decreasing the glucose concentration. Otherwise Metformin, Glyburide, Glipizide and Glimepiride are useful to reduce HbA1c as oral drugs. Among these drugs, Glyburide is more capable of reducing HbA1c when compared with other ones. We suggest the diabetic patients to use Glyburide if the diabetic case is rather bad as an oral drug. We encountered with an interesting result about Nateglinide. According to our findings, Nateglinide has negative impact on HbA1c levels of the diabetic patients. This result is opposite to published studies [20]. We also offer to investigate the impact of Nateglinide more deeply for diabetes treatment.
As our views, our findings are helpful for medical researchers in the context of diabetes mellitus. In further studies, the effects of different drugs can be also investigated together with personal factors of the patients such as gender, age, etc. on diabetes treatment.
Declaration of Interest
The authors report no conflicts of interest. The authors alone are responsible for the content and writing of this article.
References
- Bolen, Wilson, Vassy. Comparative effectiveness and safety of oral diabetes medications for adults with type 2 diabetes. Rockville (MD) 2007.
- Erdem, Dogru, Tasci. The effects of pioglitazone and metformin on plasma visfatin levels in patients with treatment naive type 2 diabetes mellitus. Diabetes Res Clin Pract 2008; 82: 214-218.
- Yamanouchi, Sakai, Igarashi. Comparison of metabolic effects of pioglitazone, metformin, and glimepiride over 1 year in Japanese patients with newly diagnosed Type 2 diabetes. Diabet Med 2005; 22: 980-985.
- Perez, Zhao, Jacks. Efficacy and safety of pioglitazone/metformin fixed-dose combination therapy compared with pioglitazone and metformin monotherapy in treating patients with T2DM. Curr Med Res Opin 2009; 25: 2915-2923.
- Nauck, Frid, Hermansen. Efficacy and safety comparison of liraglutide, glimepiride, and placebo, all in combination with metformin, in type 2 diabetes: the LEAD (liraglutide effect and action in diabetes)-2 study. Diabetes Care 2009; 32: 84-90.
- DeFronzo, Triplitt, Qu. Effects of exenatide plus rosiglitazone on beta-cell function and insulin sensitivity in subjects with type 2 diabetes on metformin. Diabetes Care 2010; 33: 951-957.
- McCullagh, Nelder. Generalized linear models. Chapman & Hall Boca Raton, Washington D.C, London 1989.
- Czepiel SA. Maximum likelihood estimation of logistic regression models: theory and implementation. CZEP 2002.
- Akaike. A new look at the statistical model identification. IEEE Transactions on Automatic Control 1974; 19: 716-723.
- Schwarz. Estimating the dimension of a model. The Annals of Statistics 1978; 6: 461-464.
- Sugiura. Further analysis of the data by Akaike’s information criterion and the finite corrections. Communications in Statistics Theory and Methods 1978; 7: 13-26.
- Bozdogan. Akaike's information criterion and recent developments in information complexity. J Math Psychol 2000; 44: 62-91.
- Deniz, Akbilgic, Howe. Model selection using information criteria under a new estimation method: least squares ratio. J Appl Stat 2011; 38: 2043-2050.
- Pamukcu, Bozdogan, Caljk. A novel hybrid dimension reduction technique for undersized high dimensional gene expression data sets using information complexity criterion for cancer classification. Comput Math Method M 2015.
- Kennedy, Eberhart. Particle swarm optimization. 1995 Ieee International Conference on Neural Networks Proceedings 1995; 1: 1942-1948.
- Lee, El-Sharkawi. Modern heuristic optimization techniques: theory and applications to power systems,, John Wiley & Sons, Hoboken New Jersey, Canada, 2008.
- Machine Learning Repository. Diabetes 130-US hospitals for years 1999-2008 data set. UCI 2016
- Strack, DeShazo, Gennings. Impact of HbA1c Measurement on hospital readmission rates: Analysis of 70,000 clinical database patient records. Biomed Res Int 2014.
- Bendtsen C. Particle Swarm Optimization. CRAN 2012.
- Kim, Suk, Kwon. Nateglinide and acarbose for postprandial glucose control after optimizing fasting glucose with insulin glargine in patients with type 2 diabetes. Diabetes Res Clin Pract 2011; 92: 322-328.