ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 8
Study on different meander structured microchannel: a biofilter
Saveetha Engineering College, Thandalam, Chennai, Tamil Nadu, India
Accepted date: January 17, 2017
One of the key biological materials that can be used for disease diagnosis is the blood. The first step to examine the blood is separation of molecules in blood. In this work, the meander structure based microfluidic channel with different dimensions is designed for filtering applications. The performance characteristic of microchannel is analysed for symmetric and asymmetric geometries. The geometrical parameters such as Reynolds number and friction factor is computed and plotted. The symmetric microchannel geometry with width 250 μm gives the better performance when compared to all other microfluidic channel geometries.
Keywords
Bio-molecules, Cell separation, MEMS, Microfluidics
Introduction
Clinical assays are often performed by examining the components in blood. Main components of blood are WBC, RBC, Platelets and Plasma. The preliminary step towards the blood test is the separation of bio-molecules. Size based biomolecule separation and filtration is essential for many applications such as clinical analysis, biomedical and environmental assays and micro/nano manufacturing [1-3].
Microfluidic separation techniques can be classified as active and passive methods. An active method utilizes external force such as electric field [4-7], magnetic field [8,9], acoustic wave [10,11], optical interaction [12], etc., by using the particle’s electric, magnetic and optical properties. Lack of high throughput and time consuming is the major disadvantage of active devices however they produce high separation efficacy and selectivity.
Passive devices utilize the distinct physical properties of the particle such as size, density and cell deformability [13]. These methods have the simple design and fabrication and relatively high throughput with less input volume. Different methods of designing passive devices are cross-flow filtration [14-17], deterministic lateral displacement [18], centrifugation separation [19], etc. Jafar et al. designed the microfluidic device with pillars placed in the straight rectangular channel for separation of human blood's WBC based on their size [20]. The pillars are grown with space 6 μm. Since it is a dead-end filter, the larger molecules will get blocked at the pillar. To avoid the clogging problem, Yoon et al. developed the μ- sieving technique [21]. In this technique, piezoelectric actuator induces oscillatory vibration in the channel. But it is complicated due to actuator since it need external field.
For biomedical applications, cross flow filtration technique is employed which does not involve any external device to induce the flow of particles. The principle behind this crossflow filter is that the blood is forced to flow through microfluidic channel parallel to the surface membrane rather than into the filter as in the dead-end filtration. This results in better efficiency.
Daniel et al. and Xing et al. had extracted the DNA after cell lysis by using the cross-flow filtration [22,23]. Xing et al. had separated the WBC, RBC and platelets with a tortuous channel which is made of PDMS [22]. But some particles are adsorbed on the surface of PDMS which leads to poor efficiency.
Different shapes of cross-flow based microchannels such as star shaped structure, Inverted Y-shaped structure, X-shaped structure, Z-shaped structure, sinusoidal shaped and meander shaped structure were designed and fabricated in the PDMS and the depth on PDMS layer can be varied by electrolysis process [24]. It is found that the meander shaped structure is more efficient in filtering when compared to other structures.
In this work, to have better filtering efficiency, the meander shaped microchannel is designed with different geometries. Silicon material is used in this design because of its high biocompatibility even in micro/nano sized particles. The different geometries are designed and simulated by using COMSOL Multiphysics software. And the particle flow behavior through the microfluidic channel is also observed.
Different Geometries of Meander Microchannel
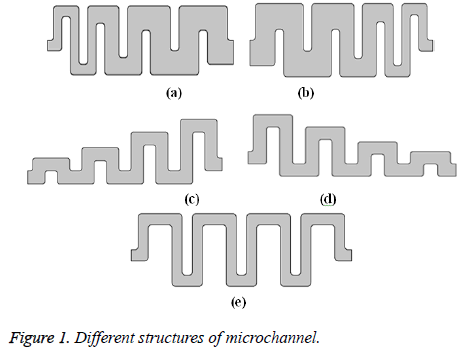
The different structure of microchannel is shown in Figure 1. Figures 1a-1d represent the microchannel with asymmetric geometries. Figure 1e represents the microchannel with symmetric geometry.
Software and Material Specification
COMSOL Multiphysics software is used for simulating and analysing the different meander structures. Laminar flow and particle tracing module is used to track the flow and particle behavior through the microchannel. Silicon material is used as it has more biocompatible properties. Properties of Silicon are given in the Table 1. The blood is chosen as a sample and its flow rate is 0.2 ml/min throughout the channel.
| Property | Name | Value |
|---|---|---|
| Density | rho | 2329 (kg/m3) |
| Dynamic viscosity | mu | 0.8 (Pa × s) |
| Thermal conductivity | K | 130 (W/(m × K)) |
| Young’s modulus | E | 170 × 109 (Pa) |
| Poisson’s ratio | Nu | 0.28 |
| Relative permeability | Mu | 1 |
| Relative permittivity | E | 11.7 |
Table 1. Properties of silicon.
Results and Discussions
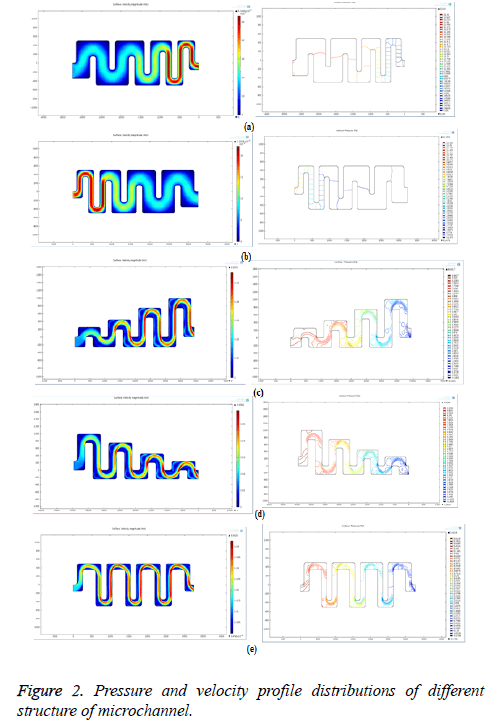
According to the Bernoulli’s principle, the velocity is inversely proportional to pressure across the channel. So when the pressure is high, the velocity (movement) of the bio-molecules in blood will be low. Creating pores where the velocity is low can give high filtering efficiency for bio-medical applications. The different structure of microchannel is designed and simulated by using COMSOL Multiphysics. The Pressure and velocity profile distribution for different structures of microchannel is shown in Figure 2.
Figures 2a-2d show the velocity profile distribution and pressure changes through the microchannel with asymmetric geometries. The velocity profile distribution from the simulation results shows the flow behavior of biomolecules through the microchannel. The velocity distribution profile depicts the non-uniform fluid flow inside the channel. But for biomedical applications, the blood flow should be laminar in order to filter the bio-molecules effectively.
Figure 2e shows the pressure and velocity profile distribution of microchannel with symmetric geometry. In this case, the initial velocity is low. Then it is increased and remains constant throughout the channel. Since it has uniform velocity, the blood flow will be more laminar. So the microchannel with symmetric geometry is suitable for designing the bio-filter.
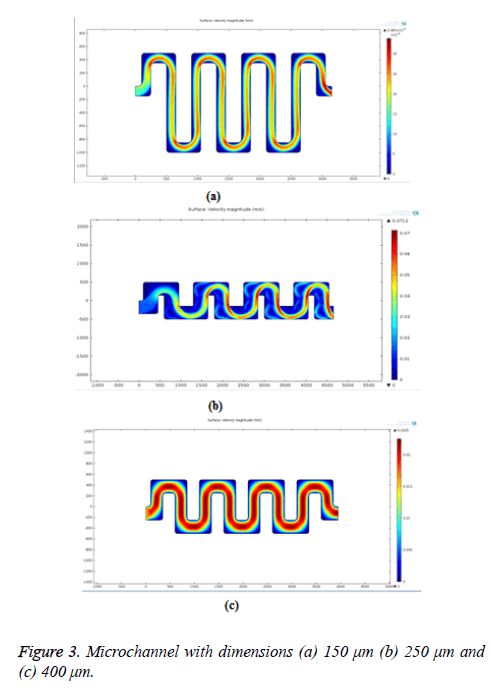
For bio-molecule separation, pores can be placed in the channel where the velocity of fluid is low. The velocity also varies depending on the dimension of the microchannel. So dimension of the structure should be determined for effective filtration. The microchannel with dimensions 150 μm, 250 μm and 400 μm were designed and simulated. The thickness of the channel is 100 μm. The gap between the parallel channels is 250 μm. The total length of the channel for width 150 μm, 250 μm and 400 μm is 9.25 mm, 9.45 mm and 9.75 mm respectively. The simulation result with various dimensions is shown in Figure 3. From the velocity profile distribution profile and pressure plots as seen in Figures 3a-3c. It is clear that the channel with width 250 μm gives the better results and flow is laminar throughout the channel.
According to Bernoulli’s principle, the pressure will be high as the velocity is low. As the velocity flow (i.e., flow rate) through the microfluidic channel at the bend is low, particles will move with reduced speed. Hence placing pores at the bends in this microchannel will acts as a biofilter for filtering applications with high efficacy.
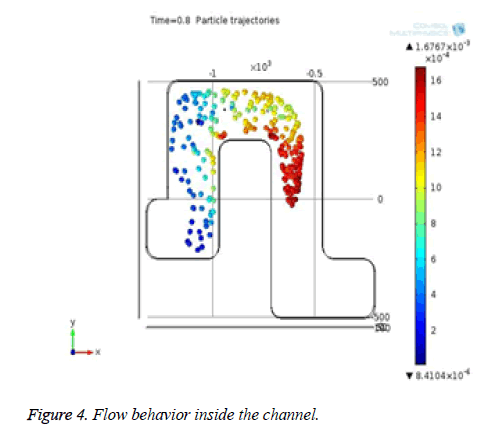
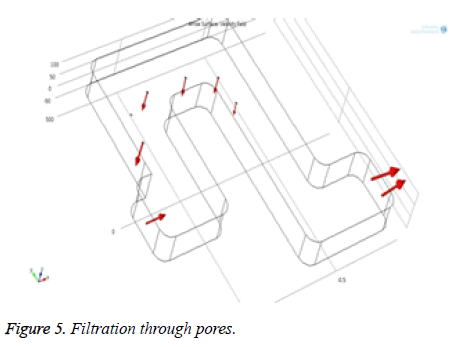
Figure 4 shows that the flow behavior of particles inside the channel and it is laminar. From the Figure 5, the red colored arrows denote the blood flow through the microchannel. Particle penetration through the pores inside the channel is also observed.
Structural Analysis
To have high efficient filtration of bio-molecules, the flow should be laminar. Reynolds number is used to find whether the flow through the channel is laminar or turbulent.
Re=ρvL/μ → (1)
Where, ρ is density of fluid
v is the velocity of fluid through the channel
L is the length of channel
μ is the viscosity of fluid
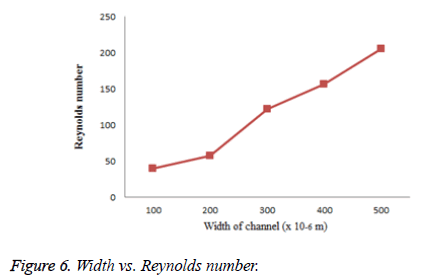
For the flow to be laminar, Reynolds number should be less than 100 in microchannel else the flow is turbulent. Reynolds number is calculated for the channel with different width such as 150 μm, 250 μm and 400 μm and is given in Figure 6.
From the above figure, it is clear that Reynolds number is increased with respect to the width of the microchannel. Reynolds number with larger width leads to a turbulent flow.
When the fluid flows through the microchannel, there will be loss. This loss can be due to friction in the channel, pressure drop and losses at the bends. For fully developed rectangular channel with laminar flow, the friction factor is calculated as
f=24/Re (1-1.3553 a+1.9467 a2-1.7012 a3+0.9564 a4-0.2537 a5) → (2)
Where,
Re is Reynolds number
a is aspect ratio
Aspect ratio depends upon the width and depth of the channel and can be calculated as
a=depth/width → (3)
The aspect ratio and friction factor for different width of the microchannel is tabulated below in Table 2.
| Width (μm) | Aspect ratio | Friction factor |
|---|---|---|
| 150 | 0.66 | 0.279 |
| 250 | 0.4 | 0.261 |
| 400 | 0.22 | 0.259 |
Table 2. Different width and its corresponding aspect ratio and friction factor.
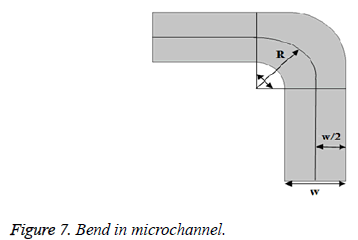
For meander structured microchannel, bend loss should be considered. Consider the single bend of the microchannel as shown below in Figure 7.
Bend loss can be calculated by using Bend loss coefficient which can be determined as
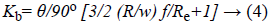
Where,
θ is the bend angle
R is the bend radius
w is the width of channel
f is friction factor
Re is the Reynolds number
By finding the loss at a single bend, it is easy to characterize the loss across the microchannel with multiple bends. Pressure drop for the rectangular microchannel is
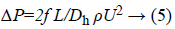
Where,
L is the length of the microchannel
Ρ is the density of fluid
U is the velocity of fluid
Dh is the hydrodynamic diameter
Dh=2wd/(w+d) Where w and d is the width and depth of the channel.
The loss due to the pressure drop is related as
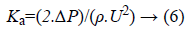
So the total loss coefficient will be the sum of the bending loss coefficient and loss due to the pressure drop. The bending loss and loss due to pressure drop for a single bend is tabulated below in Table 3. From the mathematical analysis, it is observed that when the width of the channel is increased, friction factor, pressure drop and losses due to bend decreases.
| Width (μm) | Bend loss coefficient (× 103) | Pressure drop (Pa) | Pressure drop loss coefficient |
|---|---|---|---|
| 150 | 7.48 | 99.34 | 86.148 |
| 250 | 5.29 | 79.12 | 68.613 |
| 400 | 4.40 | 72.80 | 63.132 |
Table 3. Bending and pressure drop loss.
Conclusion
Thus the performance of microchannel is studied for symmetric and asymmetric geometries. The geometrical parameter such as Reynolds number and friction factor is computed. The geometrical parameter and flow behavior of symmetric microchannel with width 250 μm gives the desired laminar flow for filtering applications. Placing different sized pores at each bend acts as a biofilter for filtering RBC, WBC, and Platelets.
References
- Mark DT, Nicole P. Microfluidic platform for performing surface-based clinical assay. Exp Rev Mol Diagn 2011; 11: 711-720.
- Jivani RR, Lakhtaria GJ, Patadiya DD, Patel LD, Jivani NP. Biomedical microelectromechanical systems (BioMEMS): Revolution in drug delivery and analytical techniques. Saudi Pharm J 2016; 24: 1-20.
- Kisore KRT, Vijayalakshmi MA. A review on recent developments for biomolecule separation at analytical scale using microfluidic devices. Analytica Chemica Acta 2015; 906: 7-21.
- Peng Z, He N, Mi JL, Seong HK. Ultra-fast separation of infectious disease-related small dna molecules by single and multi-channel microchiop electrophoresis. Elsevier 2013; 106: 388-393.
- Yuta N, Sakiko H, Takashi Y. Blood plasma separation and extraction from a minute amount of blood using dielectrophoretic and capillary forces. Sens Actu 2010; 145: 561-569.
- Bobby M, Anas A, Ghulam D, Hyung JS. Dielectrophoresis based cell switching in continuous flow microfluidic devices. J Electrostat 2016; 84: 63-72.
- Chaohui W, Xiazhang W, Zhuangde J. Dielectrophoretic driving of blood cells in a microchannel. Biotech Biotechnol Equip 2011; 25: 2405-2411.
- Jung Y, Choi Y, Han KH, Frazier AB. Six-stage cascade paramagnetic mode magnetophoretic separation system for human blood samples. Biomed Microdevices 2010; 12: 637-645.
- Pamme N, Eijkel JCT, Manz A. On-chip free-flow magnetophoresis: Separation and detection of mixtures of magnetic particles in continuous flow. J Magnet Magn Mater 2006; 307: 237-244.
- Alireza B, Hossein P, Mohsen J, Aminollah M, Peiman M, Alireza FT, Amir SN. Microfluidic intergrated acoustic waving for manipulation of cells and molecules. Biosens Bioelectr 2016; 85: 714-725.
- Fong EJ, Johnston AC, Notton T, Jung SY, Rose KA, Weinberger LS, Shusteff M. Acoustic focusing with engineered node locations for high-performance microfluidic particle separation. Analyst 2014; 139: 1192-1200.
- Lin YH, Lee GB. Optically induced flow cytometry for continuous microparticle counting and sorting. Biosens Bioelectron 2008; 24: 572-578.
- Elodie S, Herve R, Patrick P, Yves F, Jean LA. Passive microfluidic devices for plasma extraction from whole human blood. Sens Actu 2009; 141: 617-624.
- Crowley TA, Pizziconi V. Isolation of plasma from whole blood using planar microfilters for lab-on-a-chip applications. Lab Chip 2005; 5: 922-929.
- Ji HM, Samper V, Chen Y, Heng CK, Lim TM. Silicon-based microfilters for whole blood cell separation. Biomed Microdevices 2008; 10: 251-257.
- VanDelinder V, Groisman A. Separation of plasma from whole human blood in a continuous cross-flow in a moulded microfluidic device. Anal Chem 2006; 78: 3765-3771.
- Chen X, Cui DF, Liu CC, Li H. Microfluidic chip for blood cell separation and collection based on crossflow filtration. Sens Actuator B 2008; 130: 216-221.
- Davis JA, Inglis DW, Morton KJ, Lawrence DA, Huang LR. Deterministic hydrodynamics: taking blood apart. Proc Natl Acad Sci USA 2006; 103: 14779-14784.
- Blattert C, Jurischka R, Tahhan I, Schoth A, Reinecke H. Improved plasma yield by a new design of microchannel bend structures. Proc Micro Tot Anal Systems 2006; 359-361.
- Alvankarian J, Bahadorimehr A, Yeop Majlis B. A pillar-based microfilter for isolation of white blood cells on elastomeric substrate. Biomicrofluidics 2013; 7: 14102.
- Yoon Y, Kim S, Lee J, Choi J, Kim RK. Clogging-free microfluidics for continuous size-based separation of microparticles. Sci Rep 2016; 6: 26531.
- Xing CDC, Haoyuan CHL, Jianhai S, Lulu Z. MEMS-based microdevice for cell lysis and DNA extraction. Chin Acad Sci 2008.
- Chen X, Cui D, Liu C, Li H, Chen J. Continuous flow microfluidic device for cell separation, cell lysis and DNA purification. Anal Chim Acta 2007; 584: 237-243.
- Jianliang Y, Luis F, Muthukumaran P, Ion S. Modeling the effect of channel bends on microfluidic flow. Micromechatronics Lab 2005.