ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 9
Simulation of HIV/AIDS distribution using GIS based cellular automata model
1Department of Epidemiology and Medical Statistics, Chengdu Medical College, China
2Department of Applied Mathematics, Hongkong Polytechnic University, China
3Chengdu Institute of Biological Products, China
- *Corresponding Author:
- Ziqian Zeng
Department of Epidemiology and Medical Statistics
Chengdu Medical College, China
Accepted on February 4, 2017
Objective: To predict the epidemic distribution of HIV/AIDS cases in Chongqing using Cellular Automata (CA) based on the real geographic information and surveillance data. To explore a better model to simulate the transmission of HIV/AIDS based on the different epidemic parameters and initial periods.
Methods: GIS-based cellular automata models were formulated in this study, the cells were defined with regard to the real geospatial information. The distribution of HIV/AIDS was predicted and the initial value of each cell was from the real surveillance data.
Results: Six models were developed in this study under two individual epidemic parameters (0.1 and 0.05) and three initial periods (1995~2000, 1995~2001 and 1995~2002). When the individual epidemic parameter (I) was set to 0.1, with three different initial periods, the steps of iterations were 111, 103 and 91. When I was set to 0.05, the number of steps was 208, 199 and 178 respectively. The differences between predicted and real data were narrowed when the epidemic parameter was set to 0.05 and the initial period was chose from 1995 to 2002. The results showed that there was statistical significance between predicted and real distribution in four regions of Chongqing. The results, however, were improved by adjusting the individual epidemic parameter and the initial periods.
Conclusion: Our findings indicated that the models were feasible to predict the distribution, although the best epidemic parameter and initial period should be explored in further studies. The findings could provide some clues for further simulation of HIV/AIDS distribution.
Keywords
Acquired immune deficiency syndrome, Cellular automata, Geographic information systems.
Introduction
Since the first AIDS case was found thirty four years ago, the infectious cases had increased and infectious regions had enlarged dramatically [1]. From mid 90s, the incurrence of AIDs in China surged because of illegal blood transfusion [2]. The prevention and control of AIDS has already been an imperative public health issue in China, it is thus essential to obtain and understand the transmission process of AIDS.
Most of the previous studies always predicted the number of HIV/AIDS cases, even though those methods may also show the results in virtual space. Very few researchers concerned how to predict the trends of distribution of AIDS. In this study, we attempted to simulate the epidemic distribution of AIDS based on the surveillance data using the Cellular Automata (CA) models.
Cellular Automata, considered as a kind of dynamical systems, are discrete in time and space [3]. The models are used widely in medical studies. Rousseau et al. [4-6] introduced the application of CA to explore the transmission process of infectious diseases, in which, populations were subdivided into three groups: susceptible population, infective population, and immune population, parameters were set and adjusted to simulate the process of infectious diseases transmission. In 2005, Lin and Jin formulated CA models to discuss the intervention effects of quarantine in incubation and infective period using Susceptibles-Exposed-Infectives-Recovers (SEIRS) method [7].
CA models, commonly used to formulate the complex systems, are powerful in simulating the temporal and spatial evolution of spatial complex system. However, most of CA models displayed the results using the virtual spaces because of limited geography information; the implementation in the real intervention is unsatisfied.
The study proposed to formulate the CA models based geographic information system using the surveillance data of HIV/AIDS. The objectives of this study were to explore: (1) the feasibility of the method combining the GIS and CA models to simulate the transmission process of AIDS, (2) the differences of predicted results under varied epidemic parameters of transmission and different initial periods. The study, an exploratory research, aimed to provide some references for further studies.
Methods
Data source
The data involved in this study is from the center for disease control and protection in Chongqing. The information was collected from 1995 to 2009, which focused on birth data, gender, marriage, education level, occupation, infective status, route of transmission, infection date, geographic information. The geographic data was collected from national geomatics system, geographic atlas and online geomatics search system. The study coded all counties of Chongqing and divided them into four regions according to the geographic and economic information.
Formulating GIS based CA models
To understand the epidemic status of HIV/AIDS in cities, CA models were conducted based on real geographic information to simulate the distribution of HIV/AIDS in Chongqing, using software ArcGIS. The explanation of the CA models is as follows:
Cell: 1277 lattice grids are divided by 10 km × 10 kmeach grid is defined as a cell.
Cell sate: At each discrete time step, each cell is in one and only one state. Si (t) is the state of cell numbers i at the step t, represents the numbers of HIV/AIDS infectives.
Lattice: Two-dimensional geographic space in Chongqing is considered as the lattice, boundary cells are defined according to the geographic boundary, the boundary is set to the constant boundary, the state of cells outer boundary is fixed to zero.
Cell neighbors: Moore is applied to define the cell neighbors in the model with the radius of 10 km.
Rules
(1) Cells undergo random cell infection with low probability (I), supposed the initial value in one cell is Si (t), then the risk parameter Q [8] is calculated as follows:
(2) Moore is applied as the type of cell neighbors, central cell surrounded by eight cell neighbors, considering the self-infection; nine cells have equal probability to have new infections.
In each step, one new case was generated randomly in every nine cells with the proabilitity of Q. The formula is as follows:
Si (t+1)=Si (t)+1
If 0 case is generated in some cells, the value remains as follows:
Si (t+1)= Si (t)
End of simulation: The total values of cells are close (± 3%) to the real number of infectives in 2009.
Model fit: Firstly, comparing the real distribution and the results of simulation in the map; secondly, using the χ2 test to examine the difference between true data and simulations. Besides, considering the lack of statistic index of model fit, four regions are divided according to the geographic and economic level, using RC test to examine the difference between the true data and simulation in four regions.
Hypothesis: All death cases are ignored in the models due to the difficulties of collecting the data of death cases, there are amount of missing data in the database. According to the references, the incubation period of AIDS is reported between 10 to 12 years [9,10]. Because of that, the influencing effects caused by ignoring death cases could be accepted.
Results
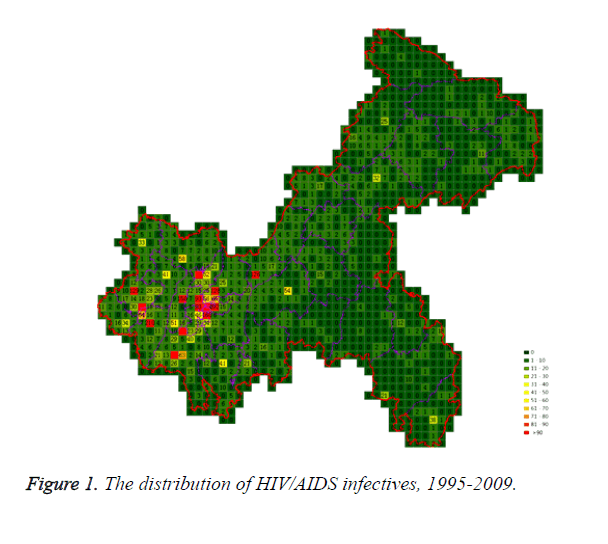
7255 infective cases were monitored from 1995 to 2009, 904 cases were deleted because of missing geographic description, 6351 cases were counted in the model eventually. Each case was located in the map of Chongqing according to the detailed geographic information, cases in each cell were counted, most cases centralized in counties coded 13, 2, 6, 37, 14, 34, 23, 12, 3, and 36 which were divided into region A and C marked with higher economic level. There were several cells with more than 90 cases, in which, the largest number in one cell was found to be 699. In Chongqing, the HIV/AIDS infectives were mostly located in central regions (Figure 1).
Cases collected during 1995-2000, 1995-2001 and 1995-2002 were analysed as initial values. Based on different individual epidemic parameters (I) and initial periods, steps and numbers of infectives were showed in Table 1.
| Initial period | I | Initial cases | No of steps | HIV/AIDS cases calculated by models |
|---|---|---|---|---|
| 1995~2000 | 0.1 | 35 | 111 | 6202 |
| 1995~2001 | 65 | 103 | 6187 | |
| 1995~2002 | 135 | 91 | 6445 | |
| 1995~2000 | 0.05 | 35 | 208 | 6494 |
| 1995~2001 | 65 | 199 | 6308 | |
| 1995~2002 | 135 | 178 | 6359 |
Table 1. Modeling results under the different epidemic parameters and initial periods.
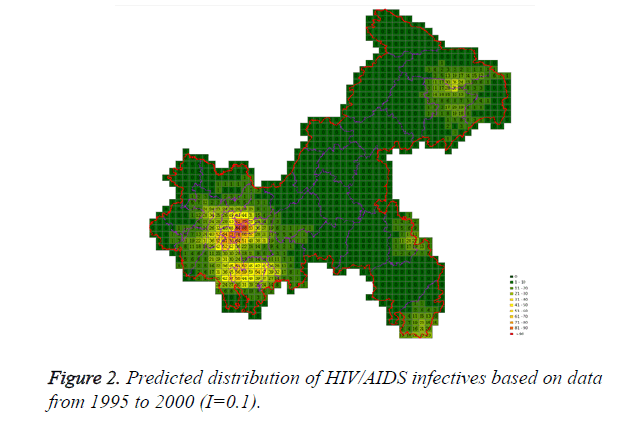
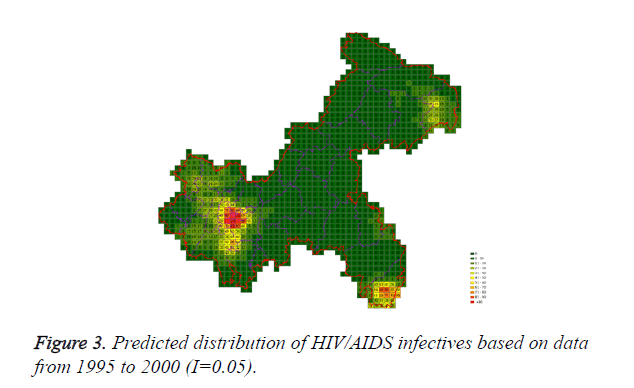
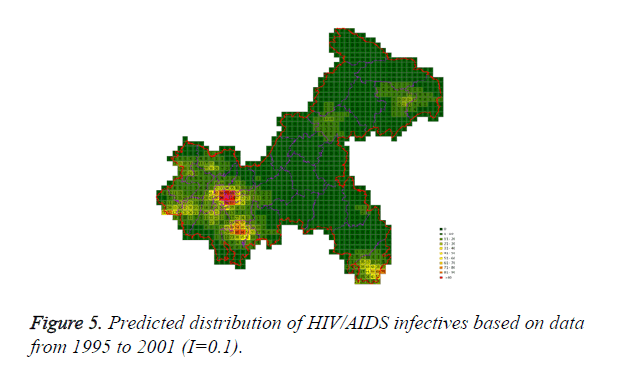
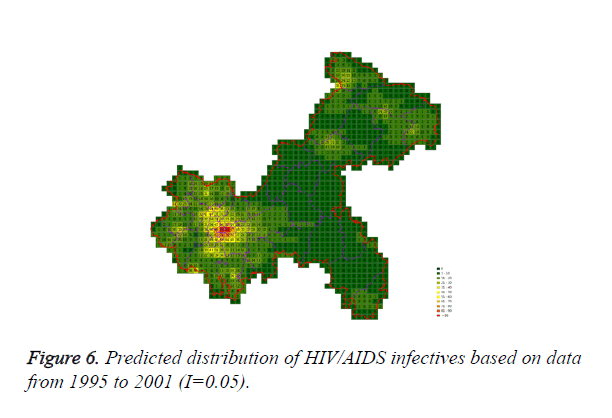
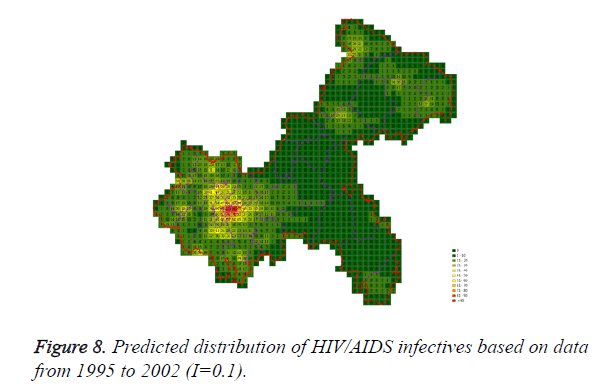
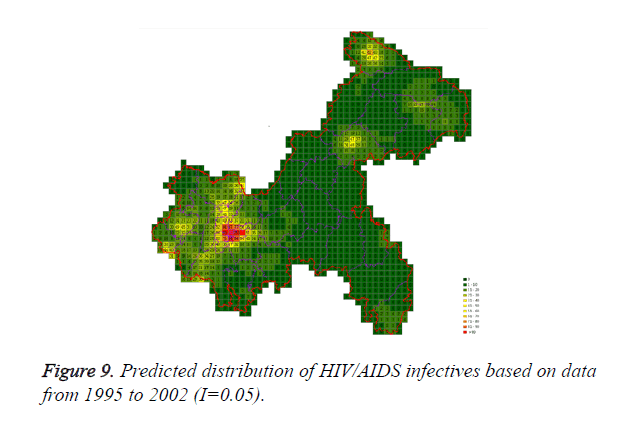
Cases located in central regions (Regions A and C) when the epidemic parameter (I) was equal to 0.1, then diffused to neighborhood gradually, the distribution of HIV/AIDS was high in central regions and decreased in surrounding area, which coincided with the true trends except the range was narrowed. Most of cases located in Region A, diffused to Region B, the trends were badly similar to the true distribution. Compared to the results of formal models (I=0.1), the distribution of cases were more centralized without exceeded diffusion, cells with large number of cases increased, which made the results closer to the true situation (Figures 2-10).
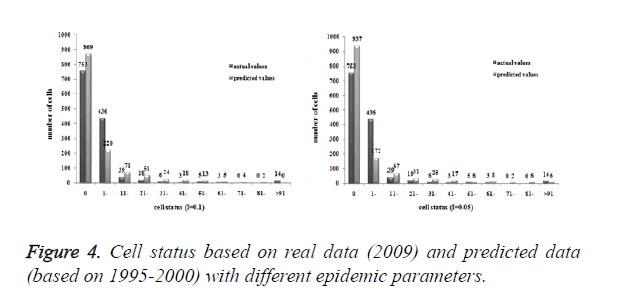
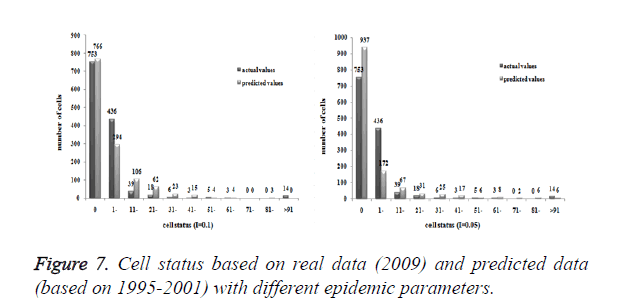
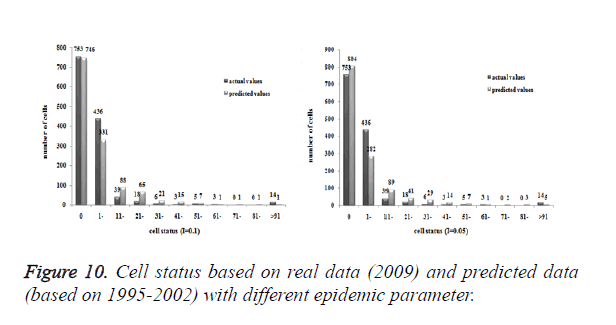
Three models were formulated based on three different initial periods, when epidemic parameter was equal to 0.1; all three simulations were generally similar with true trend, however, the fit tests of three models showed statistic difference between simulations and true trends (Table 2). With the epidemic parameter was equal to 0.05, the number of cells with more than 91 cases, increased in latter three models, statistic differences were also found according to the model fit tests. However, the χ2 values decreased significantly correlate to the longer initial periods; moreover, the model fit looked well under the epidemic parameter equal to 0.05.
| Initial period | I | Region A | Region B | Region C | Region D | Total | χ2 | P value |
|---|---|---|---|---|---|---|---|---|
| 1995~2000 | 0.1 | 2134 | 2560 | 939 | 569 | 6202 | 358.63 | <0.001 |
| 1995~2001 | 1972 | 3013 | 778 | 424 | 6187 | 237.85 | <0.001 | |
| 1995~2002 | 2452 | 2729 | 1022 | 242 | 6445 | 149.836 | <0.001 | |
| 1995~2000 | 0.05 | 2209 | 3759 | 162 | 364 | 6494 | 451.37 | <0.001 |
| 1995~2001 | 2348 | 2975 | 472 | 513 | 6308 | 180.73 | <0.001 | |
| 1995~2002 | 2460 | 2941 | 761 | 197 | 6359 | 41.83 | <0.001 | |
| Reference data | 2723 | 2862 | 570 | 196 | 6351 | - | - |
Table 2. Comparisons of real data and predicted values on the different initial periods in four regions.
Discussion
The cellular automata models were always used in the previous studies to simulate the epidemic status in lattice grid by locating the cases as the cellulars. However, in the practice, only the number of HIV/AIDS infectives was predicted in virtual space, the epidemic distribution was poorly displayed. The CA models in this study, based on the real geographic information, were formulated to simulate the epidemic distributions of HIV/AIDS in Chongqing. Combining the theory of mathematics and GIS, the expanded CA models were conducted to visualize the distribution of HIV/AIDS cases on the map. Six CA models were operated with three paired initial periods and epidemic parameters. 10 km × 10 km grid was defined as one cell in the models, the results indicated that the overall simulating distribution of HIV/AIDS were accepted, however, for some extreme high values, the differences between simulating and real data were significant.
In this study, some grids included multiple counties which may impact the accuracy of locating. Admittedly, smaller grids could obtain more accurate results, however, considering the burden of computer system, 10 km was chosen as the most appropriate dividing criteria. The results implied the distributions were similar between simulating data and surveillance data, the statistics optimised with smaller epidemic parameter or longer initial periods. Therefore, the CA models were better used in simulating for short periods.
According to the results, when the epidemic parameter was set to 0.1, the distribution of HIV/AIDS was a little bit far away from the real situation, with three different initial periods, the cases located sporadically with few extremely high values. When the value of 0.05 was chose as the epidemic parameter, the results was closer to the real distribution, which implied that 0.05 may be a better epidemic parameter to simulate the distribution based on our data in CA models.
The traditional CA theory deemed that the virtual spaces are constructed by dividing celullars to several L × L discrete grids. In the virtual spaces, data is simulated based on simple local rules. In most traditional CA models, the information of the initial infective cases, locations, and status were randomly generated by computers [7]. Unlike that, the strength of this study is to conduct the CA models to display the distribution of cases in real geographic spaces. Furthermore, this study selected the real surveillance data as the data source, which made the simulation more reliable. For the simulating process, in traditional CA models, each cell represented a suspective case; the numbers of infective cells were used to estimate the infectives. Actually, the variety of transmission routes determinate that the simulation of HIV/AIDS distribution was more complicated [11]. Thus, with hypothesizing the risk related to the status of each cell, it is more reasonable to simulate the distribution based on the real initial data and geographic information.
Conclusions
The methodology used here allowed simulating the epidemic distribution of HIV/AIDS cases in Chongqing using based on the real geographic information and surveillance data. The Cellular Automata (CA) models were proved to be feasible to predict the distribution, and further studies are expected to find the best epidemic parameter and initial period. The findings could provide some clues for further simulation of HIV/AIDS distribution.
Limitation
This study does have several limitations. The death cases were ignored in our models, which required more comprehensive information should be collected in further researches. For regions dividing, we included only two factors namely geographic location and economy level. In order to optimize the results of models, more factors should be considered, for instance, the population density, distribution of disease.
Funding
Our study is funded by the Science Foundation for technology innovative research team from Chengdu Medical College (CYTD15-06).
References
- Global HIV/AIDS response: Progress Report 2011. http://www.un.org/chinese/News/story.asp? NewsID=16740.
- Li L. Epidemiology. Beijing Peoples Med Publ H (7th edn.) 2011; 527-532.
- Bastien C, MicheI D. Cellular automata modeling of physical systems. London Cambridge Univ Press 1998.
- Rousseau G, Giorgini B, Livi R. Dynamical phases in a cellular automaton model for epidemic propagation. Physica D1997; 103: 554-563.
- Satsuma J, Willox R, Ramani A, Grammaticos B. Extending the SIR epidemic model. Physica A 2004; 336: 369-375.
- Hoya White S, Martin RA, Rodriguez Sa. Gnchez modeling epidemics using cellular automata. Appl Math Comput 2007; 186: 193-202.
- Liu QX, Jin Z. Cellular automata modeling of SEIRS. Chinses Physics 2005; 14: 1370-1377.
- Nino B, Kyeong C. Critical behaviour of a probabilistic automata network SIS model for the spread of an infectious disease in a population of moving individuals. J Phys A Math Gen 1993; 26: 3707-3717.
- Downs AM, Ancelle-Park RA, Costagliola D. Transfusion-associated AIDS cases in Europe: estimation of the incubation period distribution and prediction of future cases. J Acquir Imnlune Deric Synd 1991; 4: 805-813.
- Aleabes P, Munoz A, Vlahov D. Maturity of human immunodeficiency virus infection and incubation period of acquired immunodeficiency syndrome in injecting drug users. Ann Epidemiol 1994; 4: 17-26.
- UNAIDS Reference Group on Estimates, Modelling and Projections. Improved methods and assumptions for estimation of the HIV/AIDS epidemic and its impact: Recommendations of the UNAIDS Reference Group on Estimates. Modelling and projections. AIDS 2002; 16: l-14.