ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 16
Closed loop blood glucose control in diabetics
Faiz-Ul-Hassan, Muhammad Adil, Ali Khaqan*, Sana Shuja, Moazzam Islam Tiwana, Qadeer-ul-Hassan, Shahzad Malik and Raja Ali Riaz
Department of Electrical Engineering, COMSATS Institute of Information Technology, Chak Shahazad, Park Road, Islamabad, Pakistan
- *Corresponding Author:
- Ali Khaqan
Department of Electrical Engineering
COMSATS Institute of information Technology, Pakistan
Accepted on July 26, 2017
Diabetes is a chronic metabolic disorder affecting millions of people worldwide. Especially, type-1 diabetics have required strict glycemic control. In this paper, close loop control system is designed to normalize the high blood glucose level for diabetes patients. Glucose-insulin dynamics in blood plasma are represented by Bergman minimal mathematical model which is used as base model. The dynamical variations between different and same individual poses a major challenge in designing of controller for biological systems. The contribution of this research work lies in designing a backstepping based nonlinear controller which perfectly deals with nonlinearities present in the system. In order to visualize the robust behavior, meal and exercise are added as a disturbance factor and controller effectively track the set point value of 70 mg/dL from an initial state of hyperglycemia. The control criteria imposed on the proposed controller are hyperglycemia and hypoglycemia.
Keywords
Backstepping, Blood glucose, Diabetes, Bergman model.
Introduction
Diabetes mellitus (DM) also called diabetes, is prolonged metabolic disorder due to high blood sugar level. Diabetes is characterized by the failure of the human body to maintain the physiological ranges of blood glucose level [1]. This chronic condition occurs when pancreas inside the human body is not capable of producing enough insulin or cells are not in such a position to respond insulin properly produced by body [2]. There are over 220 million victims of this chronic disease in the world by a survey of World Health Organization (WHO).
Diabetes can be categorized mainly into two types; Type-1 Diabetes Mellitus (T1DM) and Type-2 Diabetes Mellitus (T2DM). About 1.5 million people died every year between 2000-2012 as reported in [3]. 10% of diabetics have type-1 diabetes while the rest suffer from type-2 [3]. Type 1 or insulin-dependent is the more severe form of diabetes. It usually develops in children, teenagers or at any stage of life. Therefore, also termed “juvenile” diabetes. Diabetics with type 1 lost their capability of insulin production and require continuous administration of insulin via injection or insulin pump. The symptoms of type 1 diabetes involve; frequent urination, increased thirst, increased hunger and unusual weight loss [4]. In closed loop system, insulin is delivered in continually glucose responsive way. Closed loop Artificial Pancreas Device (APD) systems normally combine three functions; (1) monitoring function using Continuous Glucose Monitor (CGM) attached wirelessly, (2) the delivery task of hormone therapy via pump (3) digital controller. Integrating aforementioned three functions provides fully automated closed loop system and these closed loop APDs are worn externally [5]. This type of closed loop system technology provides hands free, continuous glycemic control and eases the life of diabetes patients. Hyperglycemia and hypoglycemia are the two scenarios for blood glucose concentration inside the body. Hyperglycemia occurs when the sugar level is higher than 110 mg/dL and sugar level lower than 70 mg/dL referred as hypoglycemia. Both of these body’s states affect the health and life of the patient [6]. Diabetes patients manually perform the procedure of blood glucose regulation. In such scenarios, automatic closed loop controlling of sugar level permits the victims to participate in daily activities with less long terms complications. Open loop system, also defined as nonfeedback system is such type of control system in which output has no influence or effect on control action of input signal. An open loop system is considered as to follow input command or set point value regardless of final result. Closed loop system, also termed as feedback system is type of control system which takes into account current output value and changes it to the desired condition. The control mechanism in such type of systems totally dependent on output. For diabetes patients, in an open loop system, predetermined amount of insulin is injected to the patient according to the normal pancreatic insulin secretion curve. In closed loop system, sensor measures the glucose level, according to this information, control unit will inject the required amount of insulin to maintain the glucose level in normal range.
Automatic blood glucose regulation in diabetes patients is an extensive and dynamic field of research from decades. A number of efforts have been made by researchers and scientist to achieve the goal of maintaining high glucose level.
Bergman was the first person to provide more basic and physiologically verified mathematical model of blood glucose control inside a human body. It was a nonlinear single compartment model which simply uses the idea of remote tank for storing of insulin. Different mathematical variables were employed to symbolize the concentration of glucose, remote insulin and insulin in the blood plasma [7,8].
Farmer et al. discusses subcutaneous insulin vaccination which is an open loop system for providing the insulin to diabetics. To fulfil the basal prerequisite, mandatory task for the patient is to take the dosage early in the morning. Two considerations are important for this type of insulin injection stated as measurement of glucose level and an idea of how much food is to be eaten [9].
A prior model of regulating plasma glucose level, an algorithm of semi closed loop type has been presented in [10] for controlling the hyperglycemia more precisely. Authors presented Proportional Integral Derivative (PID) controller for the design of feedback system for glucose-insulin regulation mechanism in [11] where meal is to be taken into account as disturbance for the system.
An optimal neuro controller has been designed for T1DM diabetics. Linear Quadratic Regulator (LQR) control technique is employed to show the control performance of the system in the presence of large uncertainties. In this method, there is no need of online tuning of control variables [12].
In order to provide relaxation to diabetes patients for glucose intake, state estimation based approach has been investigated in [13] which perfectly deals with large time delays.
In [14], a closed loop control system for type-1 diabetics has been modeled using H∞ controller. Bergman minimal model is used for parametric representation of glucose insulin concentration. Uncertainties (meal, exercise) have been involved to visualize the robustness of the proposed system.
Another strategy for type-1 diabetics based on parametric programming was studied and analysed in detail for infusion of insulin to lower the high glucose level. Using this technique, inter-patient and intra-patient variability was minimized and optimal control input is obtained for insulin delivery [15].
Robust Fixed Point Transformation (RFPT) is used to make the Model Predictive Control (MPC) perfect robust for type-1 diabetics. Adaptive controller using RFPT technique deals with generic parameters of the system model without the need of system’s state estimation. Bergman model dynamics are perfectly validated via this transformation to control the blood glucose level of diabetics [16]. In [17], a meal detection based algorithm for continuous monitoring of blood glucose, is developed. It has high performance parameters and interpatient variability was also reduced. This methodology is perfect for artificial pancreas based control system.
Hyperglycemia can never be achieved through this method because bolus dose of insulin is infused for large meal inputs.
In the next section, Bergman glucose insulin mechanism is presented. Section III proposes the designed control law for insulin delivery. Section IV presents the discussion on obtained simulation results. Finally, section V concludes the research work.
Bergman Glucose Insulin Regulation Mechanism
Numerous efforts have been made for mathematical modeling of diabetics for glucose insulin regulation mechanism [18-20]. Dr. Bergman was one of the pioneers for developing the mathematical representation of glucose-insulin regulatory mechanism for exogenous infusion of insulin. It is also known as “minimal model” having no biological complexities.
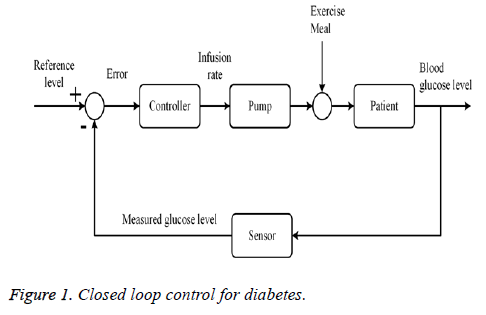
A feedback control system which measures and regulates the blood glucose concentration is shown in Figure 1. According to block diagram, a sensor will measure the glucose level and this signal will be fed back to the control system which will estimate the required exogenous infusion of insulin to normalize the glucose level. Desired amount of insulin will be provided via mechanical pump externally.
Bergman minimal model is described as follows,
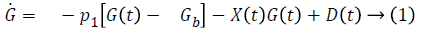
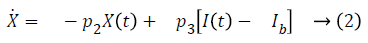
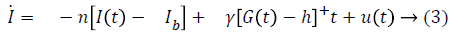
Table 1 shows the description of parameters used by Bergman.
| Parameter | Symbol | Units |
|---|---|---|
| Plasma glucose level | G (t) | mg/dL |
| Remote insulin | X (t) | mU/L |
| Plasma insulin level | I (t) | mU/dL |
| Glucose base level before injection | Gb | mg/dL |
| Insulin base level before injection | Ib | μU/ml |
| Input (insulin) | u (t) | mU/min |
| Glucose absorption rate to blood via food intake | D (t) | - |
| Insulin independent constant | p1 | 1/min |
| Decrease rate of tissue’s glucose up taking | p2 | 1/min |
| Enhanced glucose up taking capability (insulin base) | p3 | (μU/ml)/min2 |
| Plasma insulin decay rate | n | 1/min |
| Threshold value | h | mg/dL |
| Insulin secretion of β cells | γ | μU/ml/min2/(mg/dL) |
Table 1. Model parameters.
State space formation of system in Equations 1-3 is
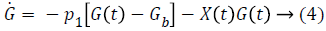
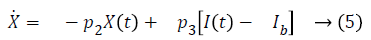
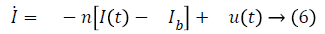
Term γ (G (t)-h)+ represents internal regulatory system which does not exist in diabetic patient, so it will be ignored. D (t) is disturbance in the form of meal or exercise, neglects it. So, Equation 6 in Laplace form is as follows
sI (s)=-nI (s)+u (s) → (7)
I (s)=u (s)/s+n → (8)
From (5),
sX (s)=-p2 X (s)+p3 I (s) → (9)
X (s)=ps u (s)/(s+p2) (s+n) → (10)
Using Equation 4,
s (G)=-p1 G (s)-Gb X (S) → (11)
G (s)=-Gb p2 u (s)/(s+p1) (s+p2) (s+n) → (12)
Transfer function of the overall system is given as
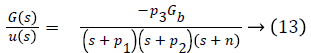
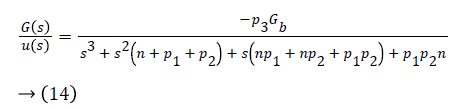
Control Law Design
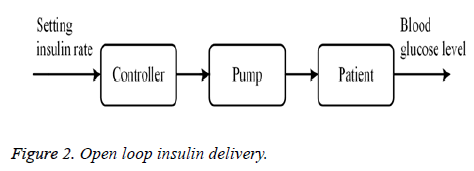
The main objective of this study is an appropriate infusion of insulin to lower the high glucose level of diabetics on priority basis. Excessive or insufficient administration of insulin may disturb physiological ranges of glucose level inside the body which affects the patient health. Insulin is infused via two methods i.e., open loop and closed loop infusion. In open loop method, a predetermine amount of insulin is injected manually. Normal pancreatic insulin secretion curve is considered as reference for insulin delivery. Figure 2 represents the open loop configuration for insulin delivery.
Close loop insulin delivery
Closed loop arrangement for insulin infusion involves a sensor which continuously measures the level of glucose. According to the information from sensor, controller decided the insulin infusion rate to normalize glucose level. Figure 1 shows close loop insulin infusion mechanism.
Proposed design
This segment presents the design of controlled input using nonlinear control technique. Since, most of the biological systems are purely nonlinear in nature on behalf of interpatient as well as intrapatient variability. In order to deal with these nonlinearities, nonlinear control technique Backstepping is used. Lyapunov function is used for stability analysis of nonlinear system around an equilibrium point. Lyapunov is a scalar function playing significant role in control theory. Backstepping is Lyapunov based nonlinear control technique. Backstepping is used for designing of stabilizing controls for a recursive class of nonlinear systems. In this process, higher order system is divided into sequence of lower order system [21]. The method of designing starts with known stable system and back out new controller which stabilizes the subsystem as well as uncertainties of main system. Recursive process is terminated when final control is achieved. Dynamical systems having nth order is decomposed into nth scalar subsystem via Backstepping and finally the synthesis of controller is implemented into nth iterations [22]. The state space model of glucose insulin regulatory mechanism is
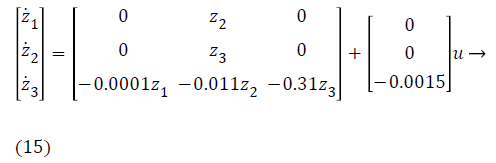
y=z1 → (16)
Where,
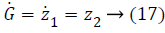
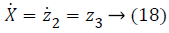
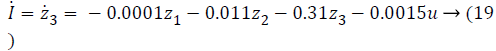
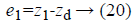
In Equations 20-22, the variables e1, e2 and e3 are error function for three states of system model, zd desired level to be tracked and a is the stabilizing function. From Equations 20-22 variables (z1, z2 and z3) can be computed as,
z1=e1+zd → (23)
z2=e2+a1 (e1) → (24)
z3=e3+a2 (e1, e2) → (25)
Step-1: Taking derivative of Equation 20 and put the value of z2, we have,
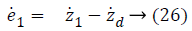
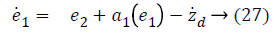
Assume the Lyapunov candidate function is
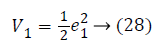
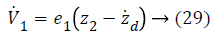
a1 (e1), used to stabilize first error state is,
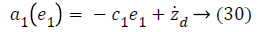
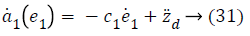
Using Equations 27 and 31 simplifies to a value for stabilizing function as
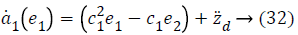
Lyapunov function simplifies to,
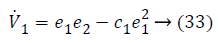
Step-2: Taking derivative of Equation 21 and put the value of z3, we have,
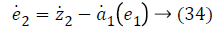
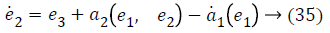
Again consider the Lyapunov candidate function is,
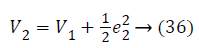
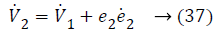
Substituting Equations 33 and 35 in Equation 37 gives,
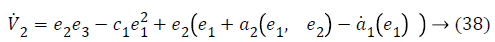
a2 (e1, e2), used to stabilize second error state is,
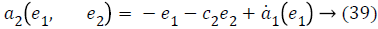
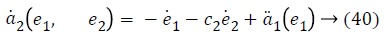
Taking derivative of Equation 32 gives the value,
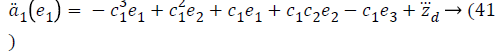
Using values from Equations 27, 35 and 41, stabilizing function reduces to a value,
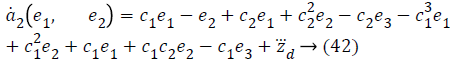
Lyapunov function simplifies to,
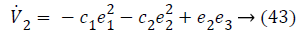
Step-3: Taking derivative of Equation 22 and substituting Equation 19, we have,
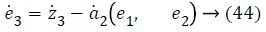
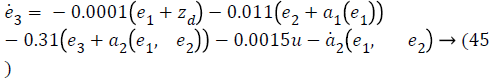
Lyapunov candidate function is,
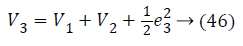
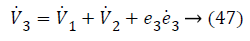
Substituting Equations 33, 43 and 45 in Equation 47; the resultant is Equation 48,
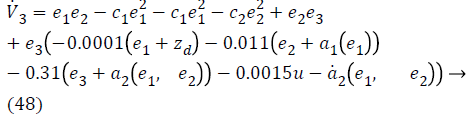
Lyapunov function simplifies to,
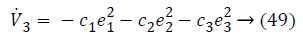
The control input for overall system is,
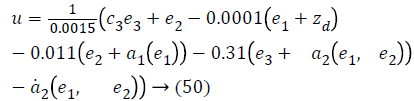
The derived control input in Equation 50 track the desired level of glucose for all diabetics in acceptable physiological range. The control law perfectly compensates the interpatient and intrapatient variability by providing insulin to control the high glucose level.
Medically, there are different states of environment in which level of glucose changes for individuals from a normal to extreme values discussed in Table 2.
| State no. | Glucose level | Clinical description |
|---|---|---|
| 1 | G ≥ 150 | Hyperglycemia |
| 2 | 150 ≥ G ≥ 110 | Slight Hyperglycemia |
| 3 | 110 ≥ G ≥ 70 | Normoglycemia |
| 4 | 40 ≥ G ≥ 70 | Slight Hypoglycemia |
| 5 | 40 ≥ 0 | Hypoglycemia |
Table 2. States of environment.
For performance evaluation of proposed controller, parameters value for different patient which were clinically investigated are shown in the Table 3 [23].
| Parameter | Normal | Patient 1 | Patient 2 | Patient 3 |
|---|---|---|---|---|
| p1 | 0.031 | 0 | 0 | 0 |
| p2 | 0.012 | 0.011 | 0.007 | 0.014 |
| p3 | 4.92-6 | 5.3-6 | 2.16-6 | 9.94-6 |
| γ | 0.0039 | 0.0042 | 0.0038 | 0.0046 |
| n | 0.265 | 0.26 | 0.246 | 0.281 |
| h | 79.035 | 80.2 | 77.578 | 82.937 |
| Gb | 70 | 70 | 70 | 70 |
| Ib | 7 | 7 | 7 | 7 |
| G0 | 291.2 | 220 | 200 | 180 |
| I0 | 364.8 | 50 | 55 | 60 |
Table 3. Parametric values.
Results and Discussion
This section presents the simulation results of Bergman minimal model using MATLAB/Simulink for designing of nonlinear Backstepping based controller. Parametric values shown in Table 3 are used for simulation purposes in order to analyse the output profile for diabetes patients.
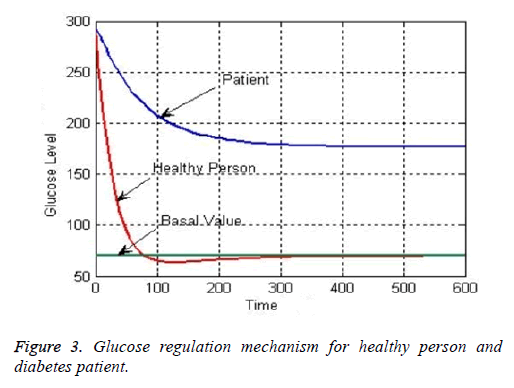
The generic profile of glucose regulation mechanism for healthy person and diabetes patient is shown in Figure 3. It can be seen from their responses that how the highly elevated level of blood glucose for healthy person tracked the desired basal value. High glucose level of healthy person slowly tracks the basal value to normalize the sugar level in physiological range. However, glucose level of diabetes patient is still very far away from the desired basal level which demands the inclusion of robust controller in the design [11].
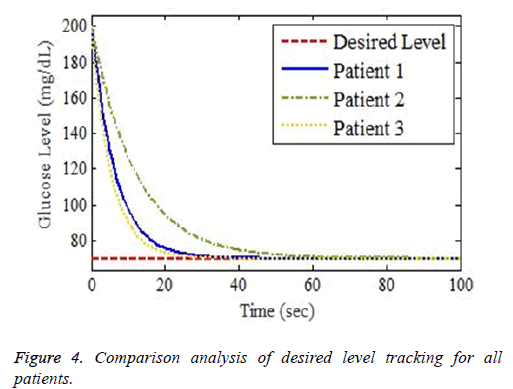
The simulation setup for desired and actual output waveforms for three different patients discussed in Table 3 is shown in Figure 4. Different clinically investigated parameters including gender, age, height and weight of patients are the main factors to be considered while attaining the desired level of glucose via designed control law. The controller also takes into consideration the interpatient and intrapatient variability while attaining the desired glucose level in normal range of 70-110 mg⁄dL.
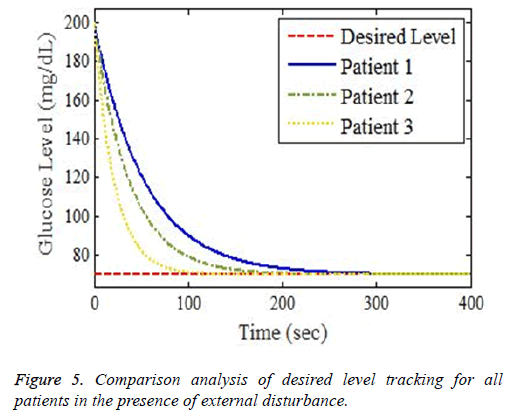
The simulation output profile for glucose level stability using proposed Backstepping based controller is shown in Figure 5. After the infusion of exogenous insulin using the derived control law, plasma glucose concentration variations and tracking of basal level has been shown in simulation results. It is evident from the obtained results that designed controller perfectly controls the high glucose level and lowers it from critical area into a stable range in an appropriate interval of time. The control law of proposed controller tracks the desired level with minimum tracking error showing the efficiency of the design.
The robustness test of proposed system can be analysed by adding disturbance factor D (t)=Aexp-Bt via controller input. This disturbance would be in the form of meal or exercise, because normal regulatory system does not exist in diabetics. The controller efficiently tracks the basal value after starting from high value of blood glucose level shown in Figure 5. Disturbance factor increases the settling time but controller track the desired level in appropriate interval of time showing the effectiveness of the proposed design. In order to achieve the desired glucose level for diabetes patients, numerous control methodologies under different control scenarios according to patient’s conditions discussed in [13-16]. The novelty of this work lies in designing of perfect robust real time controller to lower the high glucose level for diabetics in normal range. Different problems in literature review including large time delays, input uncertainties and interpatient variability has been considered preferably, and perfectly minimized. The designed controller has less settling time and minimum steady state error as compared to the other controllers, designed and discussed in previous research work before.
It can be observe that controlling the blood glucose level for three different patients in this study reveals that their output profile to attain the desired level is changing significantly. It depends on Lean Body Mass (LBM). LBM is primarily function of gender, height and weight of patients. For men and women, it is calculated as
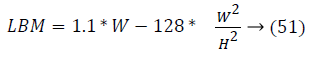
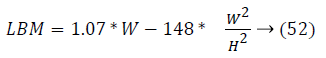
Figures 4 and 5 show different response time for three patients in order to track the desired basal level. LBM is one of the key parameter responsible for patient’s such response. The other factors are types of insulin and method through which insulin is injected into body. Types of insulin involves rapid acting, short acting, intermediate acting, long acting and infusion process includes number of insulin delivery methods like injection via syringe, insulin pens, external insulin pump, inhalable insulin and insulin jet injectors.
The combine picture of whole scenarios of desired glucose level tracking for three different patients in the presence of external disturbance is shown in Figure 5.
Conclusion
Diabetes management in human regulation mechanism is considered as one of the important and challenging task which is addressed in this paper. Bergman minimal model is used for dynamic modeling of controlling high glucose level for diabetics. Feedback linearization is employed to transform the nonlinear single compartment model into controllable canonical form. A nonlinear control scheme, backstepping is studied in detail and applied to explore different aspects of glucose regulation mechanism. The designed control law efficiently tracks the desired glucose level with minimum error for all three patients shown in Table 3. Apart from designing the control law, another important part of this research activity is the stabilizing of glucose level in the presence of disturbances (meal and exercise). Despite large inter-patient variability, as shown through the different clinical parameters of the patients, all the 3 patients achieved the desired level of glucose.
The glucose regulatory system is a vast domain in the medical field with lot of potential for real time implementation.
With the help of National Institute of Health (NIH) Pakistan, we are going to employ and test the designed control system for critically ill patients. For future work and further analysis, disturbance parameters require comprehensive study as well as application of adaptive Backstepping for the proposed system model.
References
- World Health Organization. About Diabetes 2014.
- Shoback. Greenspans basic and clinical endocrinology (9th ed). McGraw Hill Medical, New York 2011.
- World Health Organization. Global health estimates: deaths by cause, age, sex and country, 2000-2012. WHO Geneva Tech Rep 2014.
- Diabetes fact sheet No 312, WHO, 2016.
- Sara T, Annette W. Artificial pancreas device systems for the closed-loop control of type 1 diabetes. J Diab Sci Technol 2016; 10: 714-723.
- Lynch SM, Bequette BW. Estimation-based model predictive control of blood glucose in type I diabetics: A simulation study. Proceedings of the IEEE 27th Annual Northeast Bioengineering Conference, Storrs, CT, USA, 2001.
- Bergman RN, Philips L, Cobelli C. Physiological evaluation of the factors controlling glucose tolerance in man. Clin Investig 1981; 68: 1456-1467.
- Bergman RN, Finegood DT, Ader M. Assessment of insulin sensitivity in vivo. Endocr Rev 1985; 6: 45-86.
- Farmer TG, Edgar TF, Peppas NA. The future of open- and closed-loop insulin delivery systems. J Pharm Pharmacol 2008; 60: 1-13.
- Fisher ME. A semiclosed loop algorithm for the control of blood glucose levels in diabetes. IEEE Trans Biomed Eng 1991; 38: 57-61.
- Li C, Hu R. Simulation study on blood glucose control in diabetics. 1st International Conference on Bioinformatics and Biomedical Engineering 2007; 1103-1106.
- Doodnath A, Kong A, Sastry M. Optimal linear control of blood glucose. WRI World Congr Comp Sci Info Eng 2009.
- Van Rietschoten A, Singh T, Van Der Maas R. State estimations for application in diabetes control. Proc Am Control Conference 2015; 5122-5127.
- Mourad A, Keltoum G, Aicha H. Blood glucose regulation in diabetics using H8 control techniques. IET Sys Biol 2015; 2: 1-6.
- Dua P, Doyle FJ, Pistikopoulos EN. Model based blood glucose control for type-I diabetes via parametric programming. IEEE Trans Biomed Eng 2006; 53: 1478-1491.
- Gyorgy E, Jozsef KT, Levente K. Adaptive control solution for T1DM control. Applied Computational Intelligence and Informatics (SACI), 2015 IEEE 10th Jubilee International Symposium 2015; 215-220.
- Turksoy K, Samadi S, Feng J, Littlejohn E, Quinn L, Cinar A. Meal detection in patients with type-I diabetes: a new module for the multivariable adaptive artificial pancreas control system. IEEE J Biomed Health Inform 2016; 20: 47-54.
- Bolie VW. Coefficients of normal blood glucose regulation. J Appl Physiol 1961; 16: 783-788.
- Makrogluo A, Li J, Kuang Y. Mathematical models and software tools for the glucose-insulin regulatory system and diabetes. Appl Numerical Math 2006; 56: 559-573.
- Ahab AY, Kong K, Quek C. Model reference adaptive control on glucose for the treatment of diabetes mellitus. 19th IEEE Symposium on Computer-Based Medical Systems 2006; 315-320.
- Liao Y, Liao F. Design of a backstepping tracking controller for a class of linear systems with actuator delay. Math Probl Eng 2015.
- Pervaiz M, Khan Q, Bhatti AI, Malik SA. Dynamical adaptive integral sliding backstepping control of nonlinear nontriangular uncertain systems. Math Probl Eng 2014.
- Yasini S, Naghibi-sistani MB, Karimpour A. Agent-based simulation for blood glucose control in diabetic patients. Int J Appl Sci Eng Technol 2009; 5.