Biomedical Research

DOI: 10.4066/biomedicalresearch.29-17-695

Abstract

Medical imaging is a useful technique for disease diagnosis and it has many applications in the medical field. There are several techniques used for medical imaging. Among them compression sensing (CS) technique has been widely accepted because of the low sample requirement and accurate recovery of image. In this paper, a novel adaptive matching pursuit for compressive sensing of blind sparsity biological signal polluted by noise is proposed. First, the traditional quadratic loss function is replaced with the more robust Huber loss function for the purpose of combating the influence of noise. Then, sparsity adaptive matching pursuit is introduced to make optimal estimation of the original biological signal and further reduce the influence of noise, thereby achieving accurate reconstruction of biological signal with blind sparsity. Simulation results indicated that the proposed algorithm greatly improves the anti-noise performance, especially in resisting large noise uncertainty compared with existing greedy algorithms.

Keywords

Reconstruction scheme, Blind sparsity, Biological signal, Non-Gaussian noise

Introduction

Imaging has a wide range of applications in medical field such as disease diagnosis, detection, and identification of patients’ response to the therapy [1]. Image quality is vital for a Clinician to make correct clinical decisions. Shannon-Nyquist theorem aims at giving the minimal frequency needed to sample and reconstruct perfectly an analog band-limited signal [2]. Compared with the traditional Nyquist sampling theory, the compression sensing (CS) technique allows biological signal to be reconstructed using fewer samples by exploiting sparsity of the signal over a certain domain [3]. This property makes CS a promising method for collection and processing of sparse signal in recent years. Therefore, CS is widely used in biological, medical, image/signal processing and many other fields. CS is used in magnetic resonance imaging (MRI), computerized tomography (CT) scanning for image reconstruction and has been widely accepted for dealing samples which are either costly or difficult to obtain. [1,4]. Although, MRI is a widely used medical diagnostic technique, it requires long acquisition times to produce a high resolution image. The other limitations of MRI include imaging static structures over a short period, and the patient’s discomfort in holding breath during the MRI procedure [4]. By using CS technique, MRI scanners can avoid these limitations and produce images. Compressive sensing paves the way for a number of possible applications by efficiently capturing sparse and compressible signals, using a relatively small number of measurements [4]. CS techniques are capable of delivering accurate results with low radiation dose and increased imaging speed [5].

Choice of the signal’s sparse domain and measurement matrix is essential for CS. The reconstruction algorithm is the most important element of CS. Quality of signal reconstruction influences feasibility of the CS theory. In this paper, we propose an adaptive matching pursuit algorithm for biological signal reconstruction in blind sparsity. First, the traditional quadratic loss function is replaced with more robust Huber loss function for the non-Gaussian noise and the objective function based on Huber loss is constructed to improve resistance to unknown noise. Then, the sparsity-adaptive matching pursuit algorithm is used to reconstruct the sparsity-blind biological signal corrupted with non-Gaussian noise.

Methodology

Given a vector signal y with a length of n, it is sparse for a known orthogonal sparse basis 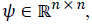and it can be written as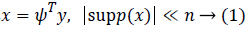

where supp(x) is the support set of x. While projecting y via the measurement matrix H, the measurements usually contain noise from the environment as

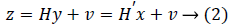
where v is the noise sequence, .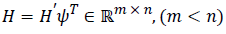

Many CS algorithms have been proposed to reconstruct the signal from noise-corrupted measurements as shown in Equation (2), most of currently available algorithms assume the noise is Gaussian. However, in the real-world environment, the measurement noise v is usually non-Gaussian [6]. To address the problem associated with non-Gaussian noise and the resultant pollution, it is very urgent to find a signal detector that can resist non-Gaussian noise. This unknown noise depends on the environment, and it may be non-Gaussian or has uncertainty, such as only part of the distribution of the noise is known. A typical model for uncertain distribution of the noise is the ε contaminated distribution [7]

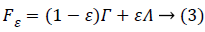
where Γ is a known Gaussian distribution, 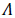is an unknown contaminated distribution, and 0 ≤ ε ≤ 1 is a known parameter which determines the ratio between Gaussian and non- Gaussian distributions.

In order to resist the ε contaminated Gaussian noise, the traditional quadratic loss function is replaced with more robust Huber loss function [7]

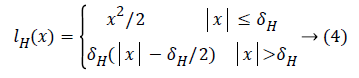
To obtain the sparse solution, the normalized l₁ norm is used here

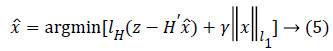
where γ is the smoothing coefficient used to balance the Huber loss function and the l₁ norm (sparsity). Equation (5) is an unconstrained convex optimization problem. It is also a nonlinear optimization problem which is not integrable at z=0, thus it does not have a global-minimal closed-form solution. But Equation (5) can be converted into a constrained optimization problem

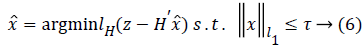
where τ is the sparsity bound of x under the l1 norm. Equation (6) indicates that lH(z-Hʹx̂) converges to a minimal value as iterations increase. Consider an extreme case where z → Hʹx̂ when the minimal value converges to 0, i.e. lH(z-Hʹx̂) → 0. In this case, the noise v is introduced to Hʹx̂, thereby, reducing the accuracy of an estimated signal 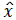and reconstructed sparse signal.

Results

Assume that the measured values are collected in the non- Gaussian noisy environment, the noise is the Gaussian-Laplace mixture, ε=0.9 and the Laplace noise parameter λ=0.2. The variance of measurement noise R_v=0.001²I_128×128, the sparse incremental step size is s=2. Reconstruction is considered successful if ||x̂-x||₂<10^-5. Each reconstruction algorithm takes 1000 times to compute the reconstruction success probability. The variance of the driving noise is Q=10I. This process can be described as

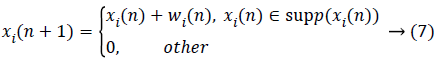
The proposed PFMP is compared with other typical methods, including MP, ROMP, SAMP, and MCMP in [6], KFCS in [8], KFMP in [9] and the BP de-noising method (BPDN) in [10].

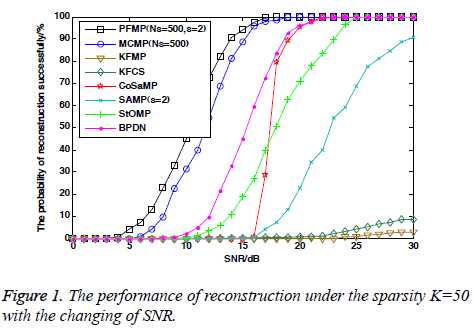
Figures 1 shows the reconstruction performance of each algorithm as a function of SNR of input measurements in the dynamic non-Gaussian noisy environment. It can be seen that even if the reconstruction performance of each algorithm is not as good as in the static environment, PFMP is still superior to others for the case of non-Gaussian noisy environment. KFCS and KFMP are still influenced by non-Gaussian noise and the performance is very poor. The performance of MCMP decreases dramatically in the dynamic environment, and is inferior to PFMP by a large margin.

Figure 1: The performance of reconstruction under the sparsity K=50 with the changing of SNR.

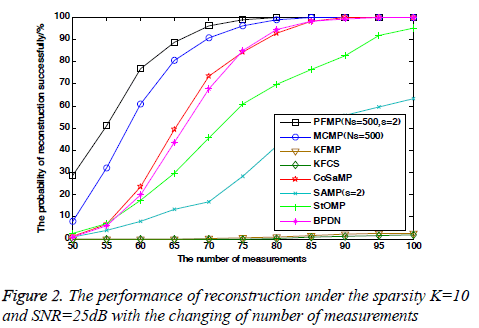
In order to evaluate further the algorithm’s reconstruction performance, Figure 2 shows the performance of all algorithms as a function of the number of measurements given sparsity and SNR. From numerical results in Figure 2, it can be observed that the reconstruction performance of each algorithm improves with the number of measurements. When the number of measurements M<90, PFMP and MCMP almost have the same performance and are both superior to others. However, as M<85, PFMP outperforms MCMP.

Figure 2: The performance of reconstruction under the sparsity K=10 and SNR=25dB with the changing of number of measurements

Conclusion

In order to improve immunity of the current reconstruction algorithm of CS with the non-Gaussian noise in the measurement, this paper proposed a particle filtering-based algorithm to reconstruct signal with blind sparsity. First, the traditional quadratic loss function is replaced with the more robust Huber loss function for the purpose of combating the influence of non-Gaussian noise, thereby achieving accurate reconstruction of signal with blind sparsity. Simulation results indicated that the proposed algorithm greatly improves the anti-noise performance, especially in resisting non-Gaussian noise compared with existing greedy algorithms.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (Grant No. 61202490) and the Henan Provincial Department of Science and Technology Research Project (Grant No. 172102210307).

References

1. Graff CG, Sidky EY. Compressive sensing in medical imaging. Appl Optics 2015; 54: C23-44.
2. Liebgott H, Basarab A, Kouame D, Bernard O, Friboulet D. Compressive sensing in medical ultrasound. IEEE International Ultrasonics Symposium (IUS) 2012.
3. Jian J, Yuan-tao G, Shun-liang M. An introduction to compressive sampling and its applications. J Elect Informat Technol 2010; 32: 447-475.
4. Baldacchini F. Compressed Sensing Techniques Applied to the Reconstruction of Magnetic Resonance Images. In: Nano-Optics: Principles Enabling Basic Research and Applications, Springer, Dordrecht, 2017.
5. Wang G, BreslerY, Ntziachristos V. Compressive Sensing for Biomedical Imaging. IEEE Transactions on Medical Imaging 2011; 30: 1013-1016.
6. Wen-biao T, Guo-sheng B, Jian K, Yang Z. Monte Carlo matching pursuit denoising inversion for compressed sensing. Acta Electronica Sinica 2015; 43: 1732-1737.
7. Huber PJ, Ronchetti EM. Robust Statistics, New Yorkm NY, USA: John Wiley & Sons Inc, 2013.
8. Vaswani N. Kalman filtered compressed sensing. 15th IEEE International Conference on Image Processing, San Diego, California, 2008.
9. Wen-biao T, Jian K, Yang Z, Guo-sheng B, Hai-bov Z. Weakly matching pursuit denoising recovery for compressed sensing based on Kalman Filtering. Acta Electronica Sinica 2014; 42: 1061-1067.
10. Carmi A, Gurfil P, Kanevsky D. A simple method for sparse signal recovery from noisy observation using Kalman filtering, RC24709(W0812-069), Armonk: IBM, 2008.