Biomedical Research

DOI: 10.4066/biomedicalresearch.29-17-761

Abstract

A self-calibration method was proposed to compensate the drawback generated by classic ellipsoid fitting algorithm. In this paper magnetometers and accelerometers were chosen to obtain geomagnetic field and gravitational field for TRIAD algorithm. The first step is using the classic ellipsoid fitting to calibrate the magnetic vector, which is taken as an internal reference in the second step. Due to the direction the geomagnetic vector and gravity vector are relatively invariant; therefore the projection of geomagnetic vector on gravitational vector is a constant value. The second step is using projection method to calibrate accelerometer. At last, both simulation and experiment were taken to prove the accuracy of the calibration method.

Keywords

Self-calibration method, Three-axis field sensors, Magnetometers.

Introduction

Biological systems including human beings produce extremely weak magnetic fields and the study of these systems is called Biomagnetism [1]. Magnetometers are the sensors used to detect the weak magnetic fields or changes in the magnetic fields. In medical field, highly sensitive magnetometers are required. SQUID magnetometer (superconducting quantum interference device) or SQUID sensors are mostly used in biomedical arena. They are used to detect minuscule changes in magnetic fields caused by nerve signals. This technique is called magnetoencephalography (MEG). MEG has great scope in neuroimaging, for example it can be used to map brain activity, to diagnose autism, and to study the pathological activity in epilepsy patients [2]. ECG is often used in Cardiology departments to diagnose patients with heart problems. Comparatively Magnetocardiography (MCG) offers significant improvements in diagnostic capability. MCG is efficient in reliable detection of non-ST-elevated myocardial infarction [3].

The complex cryogenic technology and relatively high cost involvement are the major limitations of SQUID magnetometers [4]. Magnetometers are calibrated using ellipsoid fitting algorithm. But ellipsoid fitting algorithm is mostly used to calibrate low cost navigation devices. They often generate unknown misalignment errors. In order to overcome the existing challenges, we propose a self-calibration method using Three-axial attitude determination (TRIAD) algorithm. TRIAD is a widely used algorithm to calculate the vehicle attitude which is an essential element of navigation. It was proposed in [5] by Shuster M D. The algorithm uses two or more non-parallel vectors which directions are known and invariant. The equation was given as below.

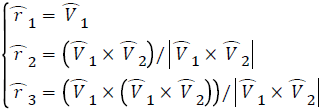(1)

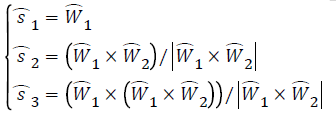
where V₁ and V₂ represent two reference vectors, and W₁ and W₂ represent the observations of them.

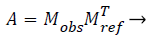(2)

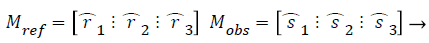(3)

where A is the transformation matrix as well as the rotation matrix. Attitude could be derived from A.

So the sensors used to obtain the vectors should be calibrated before work. In the past research, under no external cases, the errors of sensors were calibrated separately with ellipsoid fitting method which is easy and effective only to low-cost navigation devices [6]. Because it leads to a drawback that unknown misalignment error was generated among the coordinates of sensors [7]. In this paper a two-step method makes the sensors aligning to each other directly and calibrates other errors simultaneously, therefore no misalignment error was generated.

The error model of magnetometer and accelerometer were described by Fong et al. in 2008 [8]. They could be expressed with the same equation.

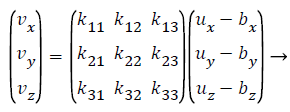(4)

where V represents the actual vector without error. U represents the measurements from tri-axial field sensor. B represents the constant error caused by hard iron and zero bias. Here K is used to represent the 3*3 matrix of k_ij, which is the actual calibration matrix combined by three parts as shown in Table 1.

Csf	Csi	Cmis

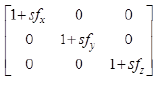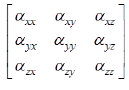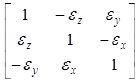Table 1. Three parts of calibration matrix.

where C_sf indicates the scalar factor calibration matrix caused by the different scalar of each component. C_si indicates the soft iron calibration matrix caused by the soft iron material around the sensor. C_min indicates the non-orthogonal calibration matrix caused by the three axes are not orthogonal to each other perfectly [9-12].

Method

Vector observations algorithm would only make sure that vector positions are relatively fixed. In this paper a novel method was proposed to fix the first vector direction using ellipsoid fitting then calibrate the second vector based on the first one. Therefore, the coordinates of two sensors are unified.

Results and Discussion

Ellipsoid fitting calibration

Ellipsoid fitting method uses the truth that the module of vector is a constant value. Substitute the equation (4) into V^TV-|V|²=0 gives,

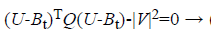(5)

where U is the measurements of magnetometer. B_t represents the constant error calculated from ellipsoid fitting. Where,

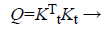(6)

where K_t represents the calibration matrix calculated from ellipsoid fitting. When K_t is diagonally dominant, Q is a positive definite matrix. So the equation (5) is the equation represents an ellipsoid.

Then Q needs to be decomposed to obtain the calibration matrix K. But when there is an orthogonal matrix represented by R, (RK_t)^T(RK_t) is also equivalent to Q. The number of R is countless, so the number of decomposition result is countless. In most past research to find a definite calibration matrix K_t would be assumed as particular form: upper triangular matrix, lower triangular matrix, or diagonal matrix. But the actual K_t may be not as same as all of them. Which is notable here, each result after decomposing could be converted to the same matrix by product R, i.e. K=RK_t. It is notable that producing an orthogonal matrix means rotation here [13-16].

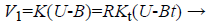(7)

The equation above shows the calibration result of ellipsoid fitting. So if the form of K_t was wrongly assumed, the calibrated vector always deviates from the actual vector by a particular angle which is constant.

Constant projection calibration

After the proceeding calibration algorithm, the calibrated magnetic was rotated a constant angle from the actual geomagnetic field. The equation of the gravitational projection on magnetic vector was given as,

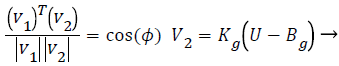(8)

where V₁ represents the pseudo vector from ellipsoid fitting algorithm. V₂ represents the actual vector, K_g represents the calibration matrix from constant included angle algorithm. Then substitute the equation (8) into (9) gives,

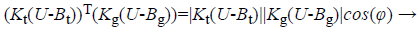(9)

The right side of the equation is a constant value.

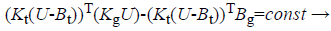(10)

Accordingly, using the outputs of tri-axial field sensor and the classic least square algorithm could obtain K_g and B_g.

Simulation: Assuming that the first vector is the geomagnetic field vector which is represented by h=(0.8 0 0.6)nT, the second vector is the gravitational field vector which is represented by g(0 0 1) m/s². The Gaussian wideband noise of magnetometer was N~(0,0.01²)n^T. To verify the algorithm proposed in this paper K was set as an irregular matrix as shown in Table 2.

	Kt	Bt
Magnetometer
Accelerometer

Table 2. Calibration matrix of magnetometer and accelerometer.

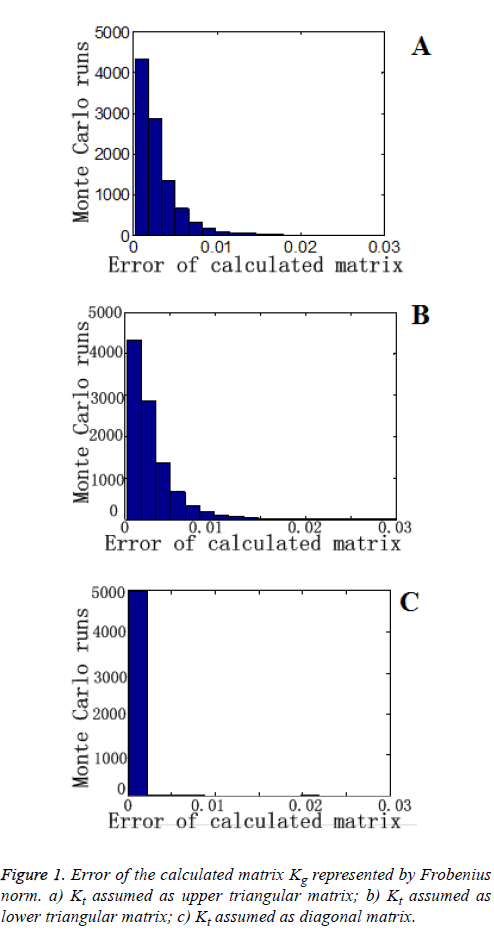
Here, use the Frobenius norm to evaluate the error between the matrix calculated and the matrix we set.

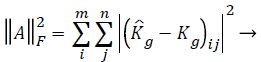(11)

where K_g represents the calculated matrix from proposed algorithm.

The results from 10000 Monte Carlo runs were given as below. Table 3 shows the ellipsoid fitting calibration result of accelerometer. And the lower triangular matrix is the transposition of upper triangular matrix.

	Kg	Bg
Upper triangular matrix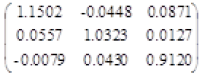
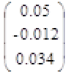Diagonal matrix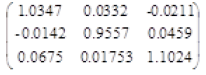

Table 3. Calibration matrix of accelerometer from calculation.

Figure 1 shows that no matter what form that the decomposition chooses, the method proposed in this paper could obtain the calibration matrix of the second vector accurately. Then two vectors’ direction would always be relatively invariant.

Figure 1: Error of the calculated matrix Kg represented by Frobenius norm. a) Kt assumed as upper triangular matrix; b) Kt assumed as lower triangular matrix; c) Kt assumed as diagonal matrix.

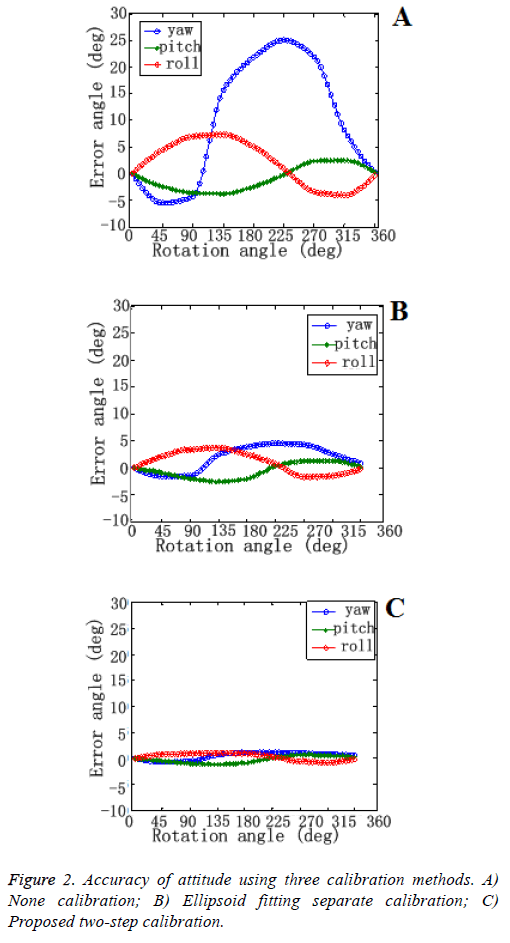
Experiment: To verify the ellipsoid fitting an ADXL345 with a resolution of 10 mg and a HMC5883 with a resolution of 500 nT were used to obtain the gravitational field vector and the geomagnetic field vector. Then use a non-magnetic theodolite with three degrees of freedom to provide the attitude reference which has a resolution of 0.002°. According to the simulation results, the calibration matrix of the first vector could be assumed as arbitrate form. In this section it was assumed as diagonal matrix. Two sensors were strap-down placing on the horizontal theodolite. Then the theodolite rotated 360° around the normal direction of itself and attitude was recorded at each 5°.

Figure 2 shows the experimental result calculated from TRIAD algorithm of non-calibration, ellipsoid fitting calibration separately, and two-step calibration method. It verified the accuracy and feasibility of proposed method.

Figure 2: Accuracy of attitude using three calibration methods. A) None calibration; B) Ellipsoid fitting separate calibration; C) Proposed two-step calibration.

Conclusion

The drawback of ellipsoid fitting was detailed that it could induce unknown misalignment between field sensors. Then a two-step calibration method was proposed to compensate the drawback [17,18]. Magnetic vector was calibrated at first using ellipsoid fitting which is fixed and deviated from the actual magnetic field. Then gravitational vector was calibrated with projection method accurately. Both simulation and experiment proved the accuracy of proposed method.

References

1. Shah VK, Wakai RT. A compact, high performance atomic magnetometer for biomedical applications. Physics Med Biol 2013; 58: 8153-8161.
2. http://www.todaysmedicaldevelopments.com/article/medical-device-magnetometer-vtt-research-111714/
3. Mooney JW, Ghasemi-Roudsari S, Banham ER, Symonds C, Pawlowski N, Varcoe BT. A portable diagnostic device for cardiac magnetic field mapping. Biomed Physics Eng Express 2017; 3: 015008.
4. Panina L. Electromagnetic sensor technology for biomedical applications. In: Recent Application in Biometrics, Yang and Norman, InTech, Croatia, 2011.
5. Shuster M D. Three-axis attitude determination from vector observations. J Guidance Control Dynamics 1981.
6. Gebreegziabher D. Calibration of Strap-down Magnetometers in Magnetic Field Domain. J Aerospace Eng 2006; 19: 87-102.
7. Valérie R. Complete Tri-axis Magnetometer Calibration in the Magnetic Field Domain. J Sensors 2010.
8. Fong WT, Ong SK, Nee AYC. Methods for in-field user calibration of an inertial measurement unit without external equipment. Measurement Sci Technol 2008; 19: 817-822.
9. Gietzelt M, Wolf KH, Marschollek M, Haux R. Performance comparison of accelerometer calibration algorithms based on 3D-ellipsoid fitting methods. Comput Methods Programs Biomed 2013; 111: 62-71.
10. Včelák J, Ripka P, Platil A, Kubik J, Kašpar P. Errors of AMR compass and methods of their compensation. Sensors Actuators A 2006; 129: 53-57.
11. Zhang ZQ. Two-step calibration methods for miniature inertial and magnetic sensor units. IEEE Transact Industrial Elect 2015; 62: 3714-3723.
12. Renaudin V, Afzal MH, Lachapelle G. Complete triaxis magnetometer calibration in the magnetic domain. J Sensors 2010.
13. Včelák J, Ripka P, Kubik J, Platil A, Kašpar P. AMR navigation systems and methods of their calibration. Sensors Actuators A 2005; 123: 122-128.
14. Gebre-Egziabher D, Elkaim GH, David Powell J, Parkinson BW. Calibration of strapdown magnetometers in magnetic field domain. J Aerospace Eng 2006; 19: 87-102.
15. Moulin M, Goudon JC, Marsy JM, Legendarme B, Presset R, Dedreuil-Monnet L. Process for compensating the magnetic disturbances in the determination of a magnetic heading, and devices for carrying out this process. U.S. Patent No. 4,414,753. Washington DC, U.S.A, 1983.
16. Wu Z, Wu Y, Hu X, Wu M. Calibration of three-axis magnetometer using stretching particle swarm optimization algorithm. IEEE Transact Instrument Measurement 2013; 62: 281-292.
17. Merayo JM, Brauer P, Primdahl F, Petersen JR, Nielsen OV. Scalar calibration of vector magnetometers. Measurement Sci Technol 2000; 11: 120.
18. Golub GH, Van Loan CF. Matrix computations (Vol. 3). JHU Press, USA, 2012.