Biomedical Research

DOI: 10.4066/biomedicalresearch.29-18-569

Abstract

Speckle noise is a granular disturbance, which is an inherent property in echocardiographic images. This usually degrades the image resolution and contrast. The image with speckle noise is very difficult to interpret. Despeckling is necessary to improve the visual quality for better diagnoses. In last thirty years, different methods have been proposed for despeckling of echocardiographic images. In this paper a review of these techniques is done highlighting the different types of filters and evolving approaches over last three decades. The types of filters are mainly divided into linear filers, diffusion filters and wavelet domain filters. The main aim of this paper is to do comparative study of different thresholding techniques in wavelet domain.

Keywords

Speckle noise, Echocardiographic images, Non-linear filters, Diffusion technique, Wavelet domain, Fractional calculus, Non-local mean, Bilateral filters

Introduction

Echocardiography is a technique used to get real time images of heart structure using ultrasound waves. Main advantages of echocardiography are low cost of operation, non-invasive, widely available and it causes minimal discomfort to patient. To assess the heart functionality, it is required to obtain a perfect ultrasound image of heart. Ultrasound images are mainly affected by speckle noise than additive noise. So, despeckling of ultrasound images improves the quality of images and detects the boundaries more prominently.

A wide research has been done in despeckling of ultrasound images in last couple of decades. Initially the study was focusing on linear filtering techniques. But, as speckle noise is multiplicative noise, linear filtering techniques were not able to give good quality results. It removes fine details so there are possibilities of loss of important information.

To perform the filtering, while preserving the edges and information in the ultrasound images, nonlinear filters, diffusion filters and wavelet domain filters are more suitable. In this paper we have done review of all these different techniques.

The organization of this paper is as follows. Section I describes nonlinear filters in details. Section II describes the diffusion method and advanced techniques in diffusion method. The widely used wavelet denoising method is described in section III and different thresholding techniques are described in section IV. Section V describes fractional calculus filters. The non-local mean filters and bilateral filters are described in sections VI and VII respectively. The section VIII is about results and discussion and section IX concludes this paper.

Non Linear Filters

Median filter

Median filtering is a nonlinear process useful in reducing noise and effective in preserving edges in an image by reducing random noise. It works by convolving window pixel by pixel through the image, replacing noisy value with the median value of neighboring pixels [1].

Lee filter

This filter is developed by Jong in 1981 [2,3]. The Lee filter is based on Minimum Mean Square Error (MMSE) criterion. It is better in edge preservation. The local statistics filter (Lee filter) is based on multiplicative speckle model and additive noise is considered negligible, which gives

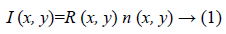
Where, I (x, y) is the Input image, R (x, y) represents the signal and n (x, y) the speckle noise. Mathematical representation for Lee filter is given in Equation (2).

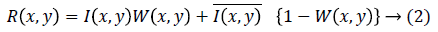
where W (x, y) is a weighting function given by

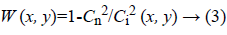
Where C_n and C_i are the coefficients of variation of the image and noise.

Kuan filter

The form of Kuan filter [4] is same as Lee filter but the W is for Kuan filter is given by Equation 4,

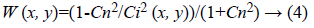
Frost filter

The Frost filter is invented in 1982 [5]. It is a linear, convolutional filter used to remove the multiplicative noise from images. Frost filter works on the basis of coefficient of variation. It is the ratio of local standard deviation to the local mean of the noised image. It gives the noise free image by convolving the input image with the spatially varying kernel. The kernel of window size n × n is moved through the image then the centre pixel value is replaced by weighted sum of values of kernel. The weighing function W (x, y) decreases as we move away from interested pixel and increases with variance. It assumes multiplicative noise. Frost filter follows formula given by Equation 5.

R (x, y)=I (x, y) × W (x, y) → (5)

Where,

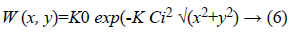
K₀-Normalizing constant, K-Controls damping rate.

The enhanced Frost and Lee filter

This filter is proposed by Lopes in 1990 [6]. It works on the basis of the threshold value. When the local coefficient of variation is below a lower threshold, averaging is done. If local coefficient of variation is above the higher threshold, it works strictly as all pass filters. And averaging and identity operation is done if the local variance is in between both thresholds. The Equation 7 for enhanced Frost and Lee filter is given below.

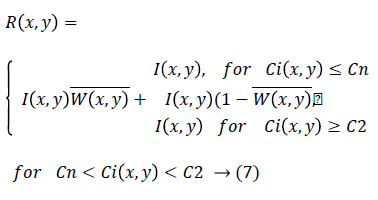
Wiener filter

Wiener filter was proposed by Norbert Wiener during the 1949. It is also known as Least Mean Square Filter. It can restore images even if they are corrupted by noise. It reduces noise from image by comparing desired noiseless image. It works on the principle of computation of local image variance. So if local variance of the image is large the de-noising is done poorly and when local variance is small we can get more accurate image. The drawback is it requires more computational time [7].

Kalman filter

The Kalman filter was first described by Kalman in 1960 and Kalman and Bucy in 1961. A2D Kalman filter has been implemented on a causal prediction window. In this filter the image is represented by a Markov field which satisfies the causal Autoregressive (AR) model. Equation 8 shows Kalman filter.

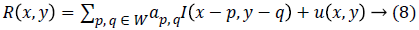
Where μ (x, y) is a noise sequence which follows the Markov process and a_p,q are the AR model’s reflection coefficients [8]. Table 1 shows the comparison of all non-linear filters.

Filter	Filtering equation	Weighing function
Median	R (x, y)=Median (I (x,y))
Lee		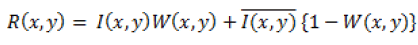W (x,y)=1-Cn2/Ci2 (x,y)
Kuan		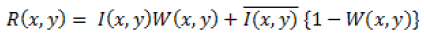W(x,y)=(1-Cn2/Ci2 (x,y))/(1+Cn2)
Frost		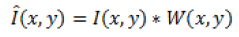W (x,y)=K0 exp(-KCi2 √(x2+y2))
Enhanced Lee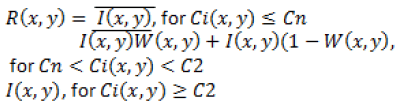
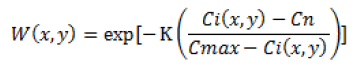Enhanced Frost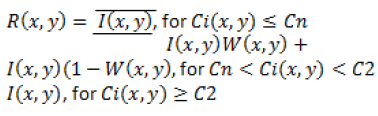
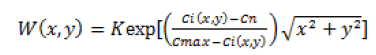Kalman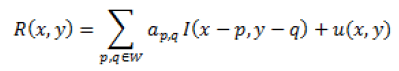

Table 1. Comparison of nonlinear filters.

Diffusion Filter

Anisotropic diffusion filter (AD)

Anisotropic diffusion filtering is method invented by Perona and Malik [9] in 1990. It is used for smoothing the image while preserving the edges. In this method, Partial Differential Equation (PDE) has been used for keeping track of homogeneous region and region containing edges in images.

The nonlinear PDE for smoothing image introduced by Perona and Malik is given in Equation 9.

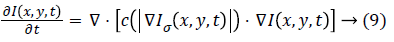
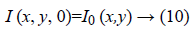
Where, I (x, y, t) is the input image for diffusion, t is time dimension representing the progress of diffusion, I₀ is the original image. and ∙() are the gradient and divergence operators, and | | represents magnitude. I_σ is a smoothed version of I. The term c (∙) represents the level of diffusion for each image position.

Perona and Malik [9] suggested two different functions for diffusion coefficients given in Equation 11.

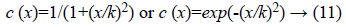
Where, k controls the level of diffusion between edges and homogeneous region in input images. To avoid over or under smoothing optimum value of c (x) should be chosen. If x>>k, Then c (x) for all-pass filter is used, whereas if x<<k, then c (x) for isotropic diffusion (Gaussian filtering) is used. The drawback of this technique is the smoothing of images with speckle noise is not satisfactory. This filtering technique enhances speckle instead of smoothing it.

Speckle reducing anisotropic diffusion (SRAD)

Yu and Acton [10] proposed new anisotropic diffusion model in 2002 to smooth speckle images. Here the diffusion PDE is used but c (∙) is a function of q i.e. the instantaneous coefficient of variation. The output image I (x, y, t) is computed using the following differential Equation 12.

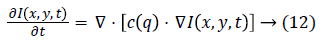
Where the diffusion coefficient c (q) is written as,

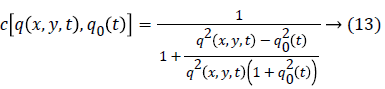
Or

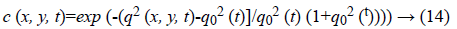
Where, q₀ is the scale function which controls the level of smoothing. In homogeneous regions, the function gives low values, and at edges or high contrast regions takes higher values.

Wavelet Denoising Technique

The wavelet transform based filtering techniques use a thresholding operator for signal denoising. These methods involve three steps: 1) the decomposition of the noisy image using forward wavelet transform; 2) the filtering of the wavelet coefficients by means of a thresholding processor; and 3) the reconstruction of image by the inverse wavelet transformation with the filtered coefficients.

The process of choosing a threshold value is a crucial task in the wavelet denoising filtering as the threshold value separates the important coefficients which are useful to reconstruct the image signal and less significant coefficients corresponding to the noise. Generally, a low threshold value preserves the details but does not reduce the noise significantly; so in this case, both the denoised and the input image with noise are very close. On the other hand, a large threshold value reduces the noise but destroys many detail coefficients with noise. To overcome these drawbacks, different thresholding rules were proposed in the literature; the most commonly used of them are summarized below.

VishuShrink or universal threshold

This technique was invented by Donoho and Johnstone [11,12] and applies the universal threshold; it consists of the use of a universal threshold defined by the following Equation 15.

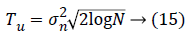
Where N is the image size and σ_n is the noise standard deviation. An estimate of the noise level σ_n is based on the Equation 16, median absolute deviation given by [13]

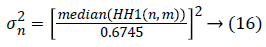
Where n and m are pixel indexes of HH1 that represents the diagonal sub-band of first level wavelet decomposition of the image. The drawback of this threshold is it removes too many coefficients that produce an excessively smoothed image because of high value of T_u.

SureShrink

This method is a combination of the universal threshold and the Stein’s Unbiased Risk Estimator (SURE) technique [14]. It computes a separate threshold for each subband and it is suited for images with sharp discontinuities; it minimizes the mean square error. This method is a level dependent threshold. In this case, the soft threshold is defined as Equation 17.

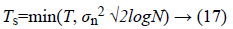
Where, T denotes the value that minimizes the SURE.

BayesShrink

This method [15] is best suited for images inculcate with Gaussian noise. For each detailed coefficients of wavelet transformed image, a threshold is estimated that minimizes the Bayesian risk. This method is better than sure shrink when compared with respect to mean square error. Retaining sharp feature is its additive advantage making it more suitable and better. The threshold is estimated by using following Equation 18.

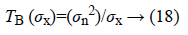
Where σ_x is the image standard deviation evaluated in each wavelet sub-band.

For the thresholding process there are two different methods which are normally used, those are described below [13].

Hard thresholding

Hard thresholding method either keeps the coefficients or kills them as shown in Equation 19, without obtaining any average or shrinked value. In this method, the coefficients are compared to an absolute threshold value and any value lower than threshold value are set to zero. It provides an advantage of edge preservation which makes it suitable in wavelet decomposition.

ht (x)=0 |x|<T

x |x|>T → (19)

Soft thresholding

In soft thresholding, the coefficients above the defined threshold value are shrinked rather then killed as in Equation 20. There is a smooth transition between obtained values and deleted values. It helps in avoiding frayed edges of the image.

st (x)=0 |x|<T

sign (x)∙(|x|-T) |x|>T → (20)

Wavelet Based New Techniques

Noval bayesian multiscale filter

Two main denoising techniques used are the thresholding technique and the Bayesian estimation shrinkage technique. Bayesian estimation technique [16] is proposed in 2001 by Achim et al. In this, for the noise-free image, it is required to consider an a priori distribution p (x) of the wavelet coefficients. If we know the likelihood function p (y/x), we can calculate the wavelet coefficients of the noise-free image by the following approaches.

1. Maximum a posteriori (MAP) estimator

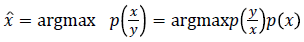
2. MMSE estimator

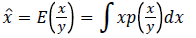
In the general case the Bayesian processor can be described as in Equation 21.

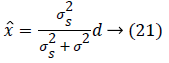
Where σ_s ² is the Gaussian signal variance. In general, the thresholding method is the discrete function which respect to threshold. But the Bayesian estimator follows a continuous shrinking function.

MRF-Based spatially adaptive Bayesian wavelet denoising

Markov Random Field (MRF) model is a promising tool for modelling images. The Bayesian estimator, combined with MRFs can generate a framework for image modeling and processing. In this study [17], Xie et al. have used an MRF to model the intrascale spatial dependence between wavelet coefficients in each individual subband. The threshold value for MRF is given by Equation 22.

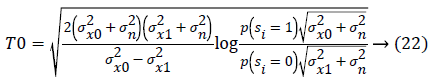
The proposed denoising algorithm proceeds as follows.

• Using the Bayesian MMSE technique estimate the shrinkage function.

• Using MAP form an initial binary mask corresponding to the hidden state configuration.

• Redefine the prior using an MRF, and then refine the binary mask by maximizing.

• Modify the shrinkage function based on the optimal binary mask.

A versatile wavelet domain noise filtration

Pizurica et al. [18] has proposed a new method in 2003, which adapts itself to various types of image noise. In this technique a single parameter is used to balance the preservation of (expertdependent) relevant details against the degree of noise reduction. The main idea of this method is the estimation of wavelet coefficients which represent signal and with noise, based on the assumption of [16] that useful wavelet coefficients persist well across the scales of decomposition described in Equation 23.

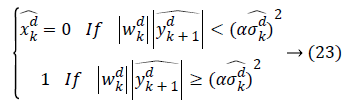
Where 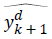is the estimate for the corresponding denoised coefficient. The thresholds are composed of α, a heuristically chosen parameter, and 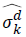an estimation of the noise level in wkd.

Nonlinear multiscale wavelet diffusion (NMWD) method

Yong [19] have developed this method in 2006 to utilize the two frequently used techniques: the wavelet denoisng technique and the iterative nonlinear diffusion method. Speckle is suppressed by implementing the diffusion process on the wavelet coefficients. With a combination of diffusion threshold strategy, the proposed method can reduce the speckle noise effectively and do auto-segmentation.

Wavelet diffusion is implemented by three steps:

• The noisy image is decomposed into the coarse scale approximation and detail images by 2-D MZ-DWT.

• Wavelet coefficients are regularized by using threshold. The threshold value is given by Equation 24.

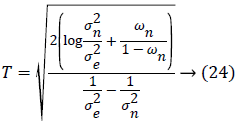
• The denoised image is reconstructed by taking the inverse MZ-DWT.

This is an iterative method, and the steps above are repeated to achieve the desired level of filtering.

Spatially adaptive filter by Bhuiyan

SNIG-Shrink method is proposed by Bhuiyan et al. [20] in 2009. In the proposed method, following steps are followed.

• The given ultrasound image is first log transformed.

• The resulting image is decomposed using wavelet transform.

• The corresponding wavelet coefficients processed by using the proposed Bayesian MAP estimator.

• The resulting output coefficients are then inversely transformed.

• Then exponential operation is performed to get the despeckled ultrasound image.

The proposed method is called SNIG-shrink, because it carries out a soft-thresholding operation with a threshold obtained from a Bayesian MAP estimator using a Symmetric Normal Inverse Gaussian (SNIG) PDF. The Equation 25 is for SNIGPDF.

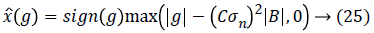
Where C is a scaling factor and B is given by SNIG PDF

The DWT is not shift-invariant, which leads to pseudo-Gibbs phenomena such as undershoots and overshoots at the locations of sharp signal transitions. These drawbacks can be overcome by implementing the denoising method using transforms such as cycle-spinning, Stationary Wavelet Transform (SWT), and dual-tree complex wavelet transform.

A suitable threshold method by Andria

The VisuShrink soft thresholding technique gives a highly impulsive distribution. Because the large value of the universal threshold sets too many coefficients to zero. To improve this drawback, a new thresholding operator was proposed [21]. The aim of the proposed method is to create an alternative function, which will be able to reduce gradually the coefficients in the zero zones. For this aim the following thresholding operator based on exponential function was defined as Equation 26.

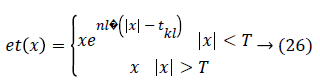
Where nl is a real parameter which finds fall degree of exponential function for l decomposition level, while kl factor provides a modified version of l-level universal threshold.

Fractional Integral Filters

Saadia et al. [22] proposed one more denoising filter using fractional calculus for echocardiographic images. Initially the image is distinguished in three regions homogeneous, detailed and edge based on gradient of intensity value. This region classification is achieved using eigenvalues of Hassian matrix. Hassian matrix is calculated for each pixel in the image. Threshold value for this classification of image is calculated using mean of eigenvalues of all pixels. After this classification image will be denoised using fractional calculus. Authors have used Grunwald-Letnikov (G-L) definition for fractional calculus. Depending upon the classified region, coefficients and order of fractional convolute mask are evaluated.

Saadia et al. [23] proposed method combining techniques of fractional integral filter and fuzzy logic to overcome the limitations of use of only fractional integral filters for speckle noise reduction in echocardiographic images. They have used proposed filter in two steps. First it utilises fuzzy logic to assign weights to the pixels in convoluting window in the image depending upon the differences in neighbouring pixels. This way, pixels are distinguished as either of same intensity regions or different (presence of edge). Then weighted mean of weights is calculated and assigned to pixel. Secondly speckle noise reduction of outcome from first stage is carried out using fractional integration filter.

Non-Local Mean Filters

The Gaussian convolution method preserves only plane zones but the detail structures are blurred or removed. On the other hand the anisotropic filter restores edges but plane zones are getting affected by noise. Antoni et al. [24] have proposed Non Local means filter which is a combination of previous methods. Non-local filters are designed to preserve edges and to remove noise from flat zones as well. This method takes the best from both the algorithms.

Jose et al. [25] have proposed a method which takes into consideration the Rician nature of the noise and spatially varying pattern of noise. They have invented Adaptive Rician Non Local Means (RNLM) Filter with Wavelet Mixing. This filter is similar to Adaptive Non Local Mean filter but with the corrected estimation of the local standard deviation of the noise σ.

In NLM algorithm, to blur sharp edges, proper weighting of the central pixel is used. To avoid overweighting, the central pixel has assigned with the maximum weight. According to [26], because of this method, the small-high contrast particles become blurred during de-noising process. To get proper details of high-contrast particles, Zang has proposed a new method called Rician NLM using Combined Patch and Pixel (RNLM-CPP).

Bilateral Filters

Ming et al. [27] states that a local neighbourhood is considered to find weighted sum of the pixels in bilateral filters. The weight is calculated from spatial distance and the intensity distance. This way we can preserve edges from blurring. In this study author has implemented bilateral filter in multiresolution analysis. It shows that we can get better results if we apply bilateral filter to approximation coefficients and wavelet thresholding to detail coefficients of an image.

The paper [28] presents a method based on bilinear filters with adaptive parameters. This method is applied to remove impulse noise and Gaussian noise simultaneously. Bilinear filter is used to remove impulse noise and Gaussian noise. To preserve edges and to make it adaptive, an Improved Artificial Bee Colony (IABC) algorithm is proposed. This algorithm finds the correct direction for search process.

Results and Discussion

The results of above discussed methods have compared in this section.

In Anisotropic Diffusion (AD) filter [9] paper, comparison of linear filters and anisotropic diffusion filters has been done. It concludes that, anisotropic diffusion is a non-linear process so it removes the trade-off between accuracy in localization and detectability; which is a main drawback of linear filters. The algorithm of AD filters is parallel so it is cheap to run on arrays of parallel processors.

Yu et al. [10] have done comparison of SRAD with anisotropic diffusion and the basic filters like enhanced Lee and the enhanced Frost filter. It is done in terms of Figure of Merit (FOM). The AD filter gives FOM of 0.4714 which is better than enhanced Lee and Frost filter. The SRAD method gives FOM of 0.7257.

In [16], the Bayesian denoising result is compared with median filter, homomorphic wiener filter and soft and hard thresholding. The result shows that, Bayesian denoising gives lower mean square error (12.7398) and higher β value (0.4559). So, this technique performs better in terms of edge preservation.

MRF-Based spatially adaptive Bayesian wavelet denoising method [17] is compared with Bayes threshold, Bayes MMSE method and refined LEE filter. The Signal to Noise Ratio is calculated for all methods. The result shows that, this method gives best SNR i.e. 2.59 among all.

Pizurica et al. [18] have done comparison between homomorphic wiener and proposed filter. The SNR of the spatially adaptive Wiener filter is 10.1 dB and; the SNR of the proposed method is SNR=12.9 dB.

The performance of NMWD algorithm [19] is compared with, the Speckle Reducing Anisotropic Diffusion (SRAD) technique, and the wavelet Generalized Likelihood ratio filtering (GenLik) method (GenLik). The results conclude that NMWD method gives better performance in terms of FOM i.e. 0.9717 which is better than SRAD (FOM=09533) and GenLik (FOM=11.88)

Gregorio et al. [20] have compared results of SNIG-shrinkI and SNIG-shrinkII with GenLik, Bayes-shrink and homomorphic Wiener filter. The result is compared in terms of Structural Similarity (SSIM). In simulation results, SNIG-shrinkI (0.8777) and SNIG-shrinkII (0.8937) gives better results.

In [21] a comparison is done with the results of Bayes Shrink method and the polynomial thresholding proposed by Smith. The proposed exponential thresholding is better in terms of β metric. But, in terms of PSNR index, the performance of proposed method and the BayesShrink is very much similar.

The method in [22] is compared with other benchmark methods like Lee, Kuan, wavelet etc. for denoising standard reference images. Proposed method has shown higher Peak Signal to Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) outperforming other methods.

Ayesha and Adnan [23] have used number of parameters to compare the results with other benchmark methods. Speckle Suppression Index (SSI) for echocardiographic image of their proposed method is 0.9647 for 4 chamber view and 0.9679 for short axis view compared to 0.97-0.98 by other benchmark methods.

In [24], the results are compared in terms of mean square error. The non-local mean filters are compared with six different filters. But, the NLM filters give the least MSE value for all the images.

The authors of [25] have compared their results with non-local mean filters, adaptive non-local mean filter and Rician nonlocal means filter. The results are compared in terms of PSNR. The results show that this method performs best for nonstationary noise as compare to other methods. It is also observed that, the proposed method performs much better than non-adaptive filters and behave much similar for adaptive filter.

Zang et al. [26] have measured results in terms of PSNR (Peak Signal to Noise Ratio) and SSIM (Structural Similarity). It was calculated to measure performance of RNLM and RNLM-CPP. With 1% of noise level, RNLM gives 33.71Peak Signal to Noise Ratio. While, RNLM-CPP gives 46.12 PSNR. The SSIM values for RNLM and RNLM-CPP are 0.9895 and 0.9989.

The results of method discussed in [27] are measured in terms PSNR. The results conclude that, the new method is 0.8 dB better than bilateral filter and 1.1 dB better than Bayes shrink. The SURE shrink gives slightly better results than the proposed method.

Yinxue et al. [28] have done performance measurement in terms of MSE, PSNR and SSIM. The proposed method is compared with alternative filters. The results shows that, BLSGSM and SURE gives better performance for images with Gaussian noise level<20. NLM and proposed method gives almost same results for many test images. But, the proposed method outperforms with the high level mixed noise.

Conclusion

We have discussed application of ultrasound image despeckling techniques in the area of echocardiography. Various influential researches in speckle reduction are presented. Traditionally used nonlinear filters with their weighing functions are discussed. Out of that the enhanced Lee and Frost filters give good results. Then we have seen that in diffusion filters, Speckle Reducing Anisotropic Diffusion (SRAD) filter is an advanced version of anisotropic diffusion invented by Perona and Malik.

We have explained the most widely used despeckling techniques. Out of which a filters using wavelet transform give the better results amongst all. This paper has given brief explanation of seven wavelet based algorithms with six different thresholding methods.

Nonlinear Multiscale Wavelet Diffusion (NMWD) method is a method which combines advantages of wavelet technique and diffusion method. According to literature [24] this is widely used method for speckle reduction. This technique can be used for image segmentation without any pre-processing.

Use of fractional calculus is discussed for echocardiographic image noise removal. This method combined with adaptive filters and fuzzy logic can greatly improve effectiveness of noise filter and its edge retention capabilities.

As compare to diffusion filters, non-local mean filters preserves edges. The RNLM-CPP algorithm preserves small high-contrast particle details too.

The bilateral filter with wavelet thresholding gives better performance in terms of PSNR. The adaptive bilateral filter can optimize the parameters and can remove noise in smooth region as well as can preserve edge details also.

References

1. Huang T, Yang G, Tang G. A fast two-dimensional median filtering algorithm. IEEE Trans Acoust Speech Sig Proc 1979; 27: 13-18.
2. Jong-Sen L. Speckle analysis and smoothing of synthetic aperture radar images. Comput Graph Image Process 1981; 17: 24-32.
3. Jong-Sen L. Speckle suppression and analysis for synthetic aperture radar images. Opt Eng 1986; 25: 636-643.
4. Kuan D, Sawchuk A, Strand T, Chavel P. Adaptive restoration of images with speckle. IEEE Trans Acoust Speech Signal Process 1987; 35: 373-383.
5. Frost VS, Stiles JA, Shanmugan KS, Holtzman JC. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans Pattern Anal Mach Intell 1982; 4: 157-166.
6. Lopes RT, Nezry E. Adaptive speckle filters and scene heterogeneity. IEEE Trans Geosci Rem Sens 1990; 28: 992-1000.
7. Garg JG, Sandeep M, Kavita CD. De-speckling of medical ultrasound images using wiener filter and wavelet transform. Int J Electron Comm. Technol 2011; 2.
8. Azimi-Sadjadi MR, Bannour S. Two-dimensional adaptive block Kalman filtering of SAR imagery. IEEE Trans Geosci Remote Sens 1991; 29: 742-753.
9. Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans Patt Anal Mach Intell 1990; 12: 629-639.
10. Yu Y, Acton S. Speckle reducing anisotropic diffusion. IEEE Trans Image Process 2002; 11: 1260-1270.
11. Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. J Am Stat Assoc 1995; 90: 1200-1224.
12. Donoho DL, Johnstone IM. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994; 81: 425-455.
13. Donoho DL. De-noising by soft-thresholding. IEEE Trans Inform Theor 1995; 41: 613-627.
14. Chang SG, Vetterli M. Spatial adaptive wavelet thresholding for image denoising. Proc ICIP 1997; 1: 374-377.
15. Chang G, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans Image Process 2000; 9: 1352-1545.
16. Achim PT, Bezarianos A. Novel Bayesian multiscale method for speckle removal in medical ultrasound images. IEEE Trans Med Imag 2001; 20; 772-783.
17. Hua X, Leland EP, Fawwaz TU. SAR speckle reduction using wavelet denoising and markov random field modeling. IEEE Trans Geosci Remote Sens 2002; 40.
18. Pizurica WP, lemahieu I, Acheroy M. A versatile wavelet domain noise filtration technique for medical imaging. IEEE Trans Med Imaging 2003; 22: 323-331.
19. Yue Y, Croitoru MM, Bidani A, Zwischenberger JB, Clark JW. Nonlinear multiscale wavelet diffusion for speckle suppression and edge enhancement in ultrasound images. IEEE Trans Med Imaging 2006; 25: 297-311.
20. Bhuiyan MIH, Ahmad MO, Swamy MNS. Spatially adaptive thresholding in wavelet domain for despeckling of ultrasound images. IET Image Process 2009; 3: 147-162.
21. Gregorio A, Filippo A, Anna MLL, Mario S. A suitable threshold for speckle reduction in ultrasound images. IEEE Trans Instrument Measur 2013; 62.
22. Ayesha S, Adnan R. Incorporating fractional calculus in echo-cardiographic image denoising. Comp Electric Eng 2018; 67: 134-144.
23. Ayesha S, Adnan R. Fractional order integration and fuzzy logic based filter for denoising of echocardiographic image. Comp Met Prog Biomed 2016; 137: 65-75.
24. Antoni B, Bartomeu C, Jean-Michel M. A review of image denoising algorithms, with a new one. SIAM J Multiscale Model Simul SIAM Interdiscip J 2005; 4: 490-530.
25. Jose M, Pierrick C, Luis M, Louis Collins D, Montserrat R. Adaptive non-local means denoising of MR images with spatially varying noise levels: Spatially Adaptive NonLocal Denoising. J Magn Reson Imag Wiley-Blackwell 2010; 31: 192-203.
26. Zhang X, Hou G, Ma J, Yang W, Lin B. Denoising MR Images Using Non-Local Means Filter with Combined Patch and Pixel Similarity. PLoS ONE 2014; 9.
27. Ming Z, Bahadir KG. Multiresolution bilateral filtering for image denoising. IEEE Trans Image Proc 2008; 17: 2324-2333.
28. Yinxue Z, Xuemin T, Peng R. An adaptive bilateral filter based framework for image denoising. Neurocomputing 2014; 140: 299-316.