ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2023) Volume 34, Issue 2
A numerical analysis of the ablation of large tumors using gamma-titanium RF electrodes.
Mohammed S Ahmed1*, Mohammed El-Wakad2, Mohammed A Hassan1
1Department of Biomedical Engineering, Faculty of Engineering, Helwan University, Cairo, Egypt
2Department of Biomedical Engineering, Faculty of Engineering and Technology, Future University in Egypt, Cairo, Egypt
- Corresponding Author:
- Mohammed S Ahmed
Department of Biomedical Engineering
Helwan University
Cairo
Egypt
Accepted date: January 19, 2023
Radiofrequency Ablation (RFA) is an alternative treatment for liver cancer to the surgical intervention preferred by surgeons. However, the main challenge remains the use of RF for the ablation of large tumours (i.e., tumours with a diameter of >3 cm). For large tumours, RFA takes a large duration in the ablation process compared with surgery, which increases patient pain. Therefore, RFA for large tumours is not preferred by surgeons. The currently materials used in RF electrodes, such as the nickel-titanium alloy (nitinol), are characterized by low thermal and electrical conductivities. On the other hand, the use of materials that have high thermal and electrical conductivities, such as titanium aluminide alloy (gamma titanium), produces more thermal energy for tumours. In this paper, we developed a cool-tip RF electrode model that uses nickeltitanium alloy and replaced it with titanium aluminide alloy by using the Finite Element Model (FEM). The aim of this paper is to study the effect of the thermal and electrical conductivities of gamma titanium on the ablation volume. Results showed that the proposed design of the electrode increased the ablation rate by 1 cm3/minute and 6.3 cm3/10 minutes, with a decrease in the required time ablation. Finally, the proposed model reduces the ablation time and damages healthy tissue while increasing the ablation volume from 22.5% cm3 to 62.5% cm3 in ten minutes compared to recent studies.
Keywords
Radiofrequency Ablation (RFA), Finite Element Model (FEM), COMSOL, Cool-tip RF.
Introduction
Liver cancer is one of the leading causes of death in both developed and developing countries. It is ranked as the fifth in terms of the most common prevalence and as the third in terms of causes of cancer-related death [1]. It is treated by surgical resection and RFA [2]. However, for large tumors, it is not preferred but surgical resection is the preferred method [3]. Surgical resection isn’t suitable for all patients due to multifocal disease, tumor size, and location of the tumor in relation to key vessels [4]. But on the other hand, for small tumors (i.e.,<3 cm in diameter), it is common to use RFA and other ablation methods such as microwave [5]. The RFA technique is the application of Radio Frequency (RF) electrical signals to soft tissue [6]. RF electrodes are injected into the organ to generate enough RF joule heating to raise the temperature above 50°C [7]. Tissues exposed to those temperatures for 1 minute or higher are destroyed by the heat [8]. This technique utilizes RF current (450- 500 kHz) to generate a thermal field required to remove a liver tumor [9]. This current passes through the organ from the active electrode to the passive electrode [10]. There are two different types of RFA techniques depending on the placement of the passive electrode: Bipolar or monopolar [11]. In the bipolar technique, electrical current passes between the two electrodes applied to the target tissue [12]. Bipolar applications are efficacious treatments for dermal defects, obesity, and sagging skin [13]. In the monopolar technique, the electrical current is connected to the organ through a small active electrode inserted into the tumor and a large electrode already present on the back of the patient [14,15]. An RF voltage is generated by an RF generator between a reference electrode and the active electrode. The electric field oscillates the alternating radio current, causing oscillatory motion of ions in the tissue commensurate with the field intensity [16,17]. Heating of tissue happens as a result of ionic excitation associated with the passage of RF current through the tissue [18]. The heat generation of tissue leads to cell dying by thermal coagulative necrosis. Therefore, RF volume thermal ablation is subject to the distribution of temperature in the tissue [19,20]. For large tumors in general, the bipolar technique is used to achieve a larger ablation volume [21]. As a result, we chose the bipolar technique because our paper focuses on large tumors. Currently, most of the commonly used RF electrodes are made of nickel- titanium alloy [22]. Nickel-titanium alloy is a very good material for medical devices because it is biocompatible with the human body [23]. However, the main limitation with nickel-titanium alloy is its low thermal and electrical conductivities [24]. Electrodes made of materials with high thermal and electrical conductivity such as gamma titanium can contribute to increased ablation volume and reduced ablation time [25].
RFA can be used for a greater number of patients and it has a greater potential for repeated treatment of tumors compared to traditional surgical resection [26,27]. The Finite Element Model (FEM) is a numerical method used to approximate the solution of boundary and initial value problems characterized by partial differential equations [28]. Lee et al., simulated medical problems about the biomechanical effects of dental implant diameter, connection type, and bone density on micro gap formation [29]. Vogel et al., [30] the authors have designed FEM to study the effects of stress and strain distribution in femoral heads for hip resurfacing arthroplasty with different materials. While, on the other hand, the authors simulated FEM to ablate bone tumor by using RFA and succeeded in abating 85% of tumor [31]. Radmilović-Radjenović M et al., [32], the authors designed FEM to ablate liver tumor by using a cool-tip RF electrode.
Several theoretical studies have studied the effect of the thermal and electrical conductivities of the RF electrode on volume ablation, including both ex-vivo [33,34] and clinical studies [35,36]. Baldelli A et al., [37] the authors compared materials that have high electrical conductivity with those that have low electrical conductivity. Xu L et al., [38] simulated RFA model using FEM two cool-tip RF electrodes made of nickel-titanium alloy. Their results showed their success in removing 4 cm3 of spherical tumor in 10 minutes, and that the best distance between two electrodes when ablation a large tumor is 1 cm. In this paper, we will use that model as a reference model.
The purpose of this paper is to use a computer model to investigate the effect of thermal and electrical conductivity for gamma titanium on ablation volume. In this paper, we designed a model based on the cool-tip RF electrode. The simulation model uses COMSOL multiphysics software to prove the possibility of reaching this goal [39]. The model is based on a numerical finite element analysis to compute the distribution of heat and electric potential inside the damage and surrounding tissue during an RF ablation. We compared both models (our developed model and the reference model) in the ablation volume values at the same time and with the same power and succeeded in abating large tumors while trying to reduce the damage to healthy cells in less time after using gamma titanium. The research is organized as follows: First, an explanation of the model's methodology, including its equations and parameters; second, the model's results and discussions, highlighting the differences in results between our model and others; and finally, the conclusions.
Materials and Methods
FEM modeling
Each FEM model is included within a cylinder domain that contains both the liver domain and the electrode domain. The radius of the base of the cylinder is 5 cm, the height is 12 cm, and the distance between the two electrodes is 1 cm [38]. Each one has the electrode geometry, RF electrode material, and liver tissue to implement. This model has four domains: The liver, electrode, trocar, and tumor domains. Finally, the effect of the following tuning parameters: Distance between two electrodes, ablation power, ablation time, and electrode design on the ablation volume is studied.
Liver domain
The liver domain includes everything surrounding the electrode, including blood, blood vessels, and liver tissues. In our study, we assumed that the tumor was spherical as 56% of liver cancer patients had spherical tumors [40]. We assumed that the tumor size was 16 cm3, which is the largest volume that has been recorded for a liver tumor in Egypt in the last ten years [41].
Electrode domains
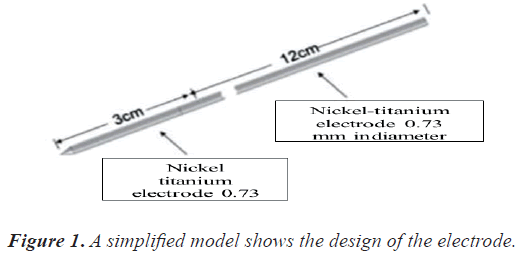
The electrode domain consists of an electrode domain and a trocar domain as shown in Figure 1 [38].
The RF electrode consists of:
• An insulated stainless-steel trocar with a diameter of 0.73 mm and a height of 12 cm
• A nickel-titanium alloy (nitinol) electrode with a height of 3 cm and a diameter of 0.73 mm with a tip in a cone
Mathematical equations
Tissue temperature change due to RF can be mathematically explained by the following Pennes equation [42].
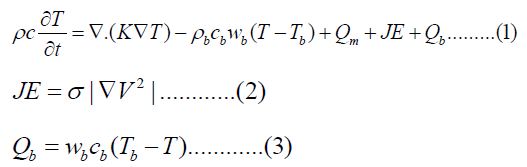
where r is the is the tissue density (kg/m3), c is tissue specific heat capacity (J/kg/K), κ is tissue thermal conductivity (W/m/K), wb is blood perfusion rate (1/s), and Qm is the volumetric heat produced by metabolism (W/m3).
JE is joule heating, which represents heat generated by RF, where J is current density, E is electric field intensity, σ is conductivity with a unit of Sm-1 and V is voltage impressed on the electrode.
Qb is volumetric heat produced by radiofrequency heating (Wm-3) calculated using equation (2), Tb is core blood temperature (supposed to be 37°C), because the blood vessels effect was discarded in this study then we can assume Tb and T are equal then Qb was set to zero Wm3.
The RF operating frequency is approximately 450-500 kHz, that is usually used for bipolar technique [43]. Depending on this, the main mode of the RF electrode during power delivery is conduction with low capacitance coupling. In this case, the model can be considered as a semi-electrostatic field [44].
Heat of resistance can be generated as a result of the action of an electrical field resulting in the thermal field of the coupling [45]. These two fields have a concerted influence on the division of the heat field and the electric potential field via the liver model [46]. Equations (1-3) offer solutions to problems associated with electro-thermal in RFA.
Materials and boundary conditions
Depending on the literature, the physical characteristics of the reference model are shown in Table 1 [47,48].
| Tissue | Electrical conductivity (S/m) | Specific heat (J/kg.K) | Thermal conductivity (W/m.K) | Density (kg/m3) | Blood perfusion ( s-1) |
|---|---|---|---|---|---|
| Liver | 0.333 | 3600 | 0.512 | 1060 | 0.0017 |
| Tumor | 0.1168 | 4200 | 0.552 | 999 | 0.0156 |
Table 1. Electrical and thermal properties of the materials.
The first value voltage and the first value temperature of the whole FEM model were taken as 0 V and 37°C, respectively. The liver and tumor have blood perfusion values because they have contact with blood, while the electrode and trocar do not have blood perfusion values because they do not have contact with blood. The surface of the liver was considered insulated and grounded, and the surface of the electrode was voltage loaded V0
V=0 on the surface of the liver ………… (4)
V=V0 on the surface of the electrodes ………… (5)
n.j=0 on all other boundaries ……… (6)
V0 in our model varied from 22 to 30 volts applied to the RF electrode.
Tuning parameters of the model
Understanding the parameters that influence the volume of RF thermal ablation is critical for designing a probe and generator formations that best suit the patient anatomy and clinical goals.
The best way to solve this issue may rely on the application of two RF electrodes. In order to achieve this goal, we have selected three main parameters as follows.
Ablation power
Ablation power is related to the amount of energy required to ablate the tumor as follows [49].
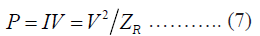
Where ZR is the tissue impedance between RF electrodes
Usually, the value is 5 joules with direct current charged on the RF electrode [50]. We can increase or decrease the power by changing the value of joules.
Ablation time
Time ablation is the time required to perform the ablation process of the tumor [51]. The ablation time ranges from one to ten minutes.
Electrode design
The electrode design and its material have an important role in increasing the volume of tumor ablation. In this study, we developed the electrode design by using titanium aluminide alloy (gamma titanium) instead of the nickel- titanium alloy. This titanium alloy is biocompatible and has superior corrosion resistance, high specific strength, rigidity, lower density, and higher thermal and electrical conductivities than nitinol, as shown in Table 2 [52]. Then, we modified the diameter of the active part from 0.73 mm to 1 mm and the height of the cone from 1 mm to 6 mm to be suitable for large tumors.
| Material | Nitinol | Gamma titanium |
|---|---|---|
| Electrical conductivity (S/m) | 9.8 × 105 | 9.56 × 106 |
| Specific heat (J/kg.K) | 500 | 620 |
| Thermal conductivity (W/m.K) | 36.7 | 124 |
| Density (kg/m3) | 8100 | 4700 |
Table 2. Properties of the nitinol and gamma titanium materials [53, 54].
Ablated tissue
Healthy cells are differentiated from ablated cells by Healthy cells are differentiated from ablated cells by
• The hyperthermia damage temperature (Td,ℎ).
• The cryogenic damage temperature (Td,).
• Instantly after the temperature exceeds the hyperthermia necrosis temperature (Tn,h).
• Instantly after the temperature falls below the cryogenic necrosis temperature (Tn,).
Then the damaged tissue indicator, α, defined either by
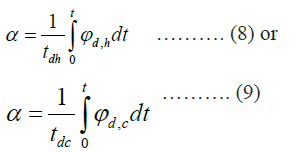
where ϕd ,h is the period of time when T>Td,ℎ to thetime limit tdℎ and the ratio of the period of time when T>Td,h to the time limit tdh.
The value of the damage indices (α) is set to one for healthy cells and zero for damaged cells. When the ablation process starts, damaged cells are removed, and the value is converted from zero to one according to the following equations.
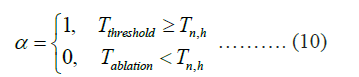
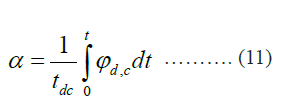
After the time of ablation reaches 10 minutes, we computed the ablation volume at various times to evaluate the integrations of areas of damage.
Results and Discussion
At the beginning, for both two models, we increased the power value from five joules to 10, 12.5, and 15 joules to increase the ablation volume and decrease the ablation time.
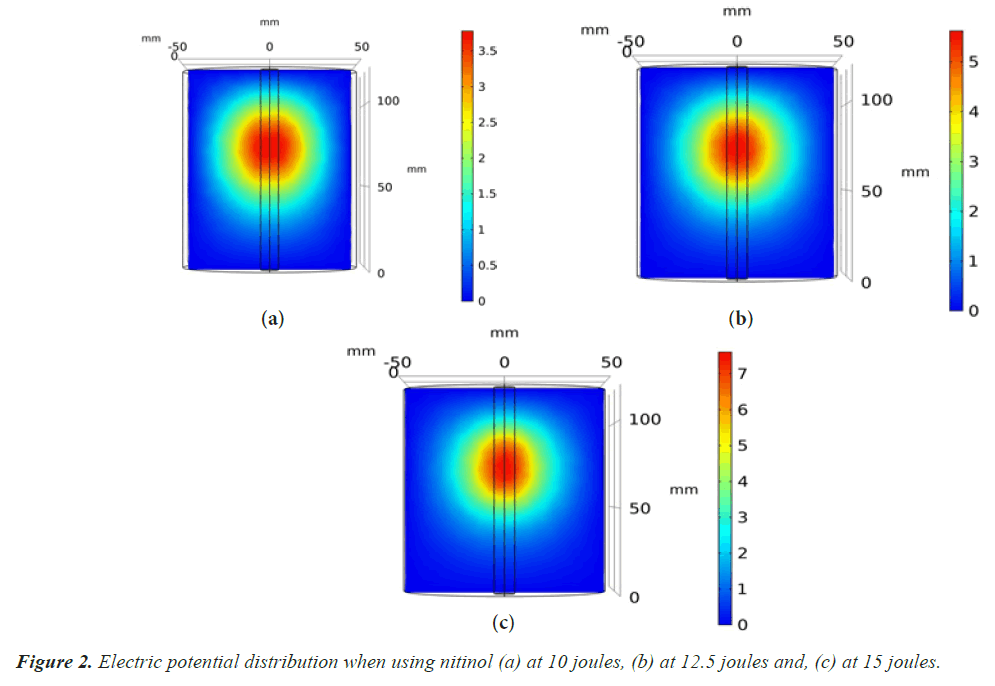
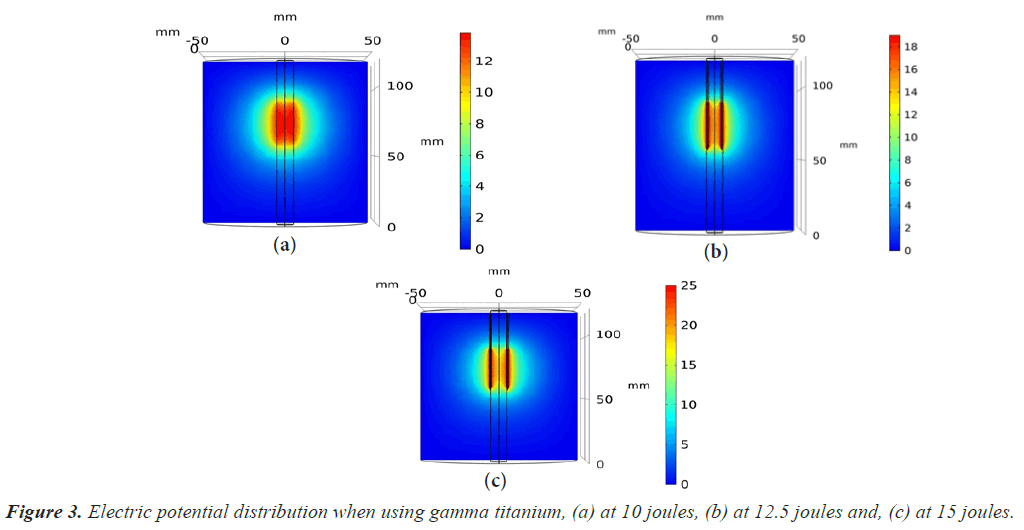
The electric potential field distribution was shown after 10 minutes, as shown in Figures 2 and 3. We increased the voltage of the electrical potential value from 3.5 V to 25 V after the development of an RF electrode design, which helps to increase the ablation volume. Then we began to calculate the ablation volume by changing the values for the ablation time and the ablation power. By calculating the ablation volume after the development that we made and comparing it before the development, we found that the ablation volume increased as shown in Tables 3-5 respectively.
| Time (min) | Power (Joules) | Volume (cm3) with a nickel-titanium alloy | Volume (cm3) with a gamma titanium | Rate of increase (cm3) |
|---|---|---|---|---|
| 1 | 10 | 0.5 | 1.4 | 1 |
| 2.5 | 10 | 1.5 | 2.4 | 1 |
| 5 | 10 | 2.4 | 3.4 | 1 |
| 7.5 | 10 | 2.9 | 4.1 | 1.2 |
| 10 | 10 | 3.4 | 5 | 1.6 |
Table 3. Ablation volume at 10 joules and the rate of increase in the ablation volume.
| Time (min) | Power (Joules) | Volume (cm3) with a nickel-titanium alloy | Volume (cm3) with a gamma titanium | Rate of increase (cm3) |
|---|---|---|---|---|
| 1 | 12.5 | 0.5 | 2.7 | 2.1 |
| 2.5 | 12.5 | 1.3 | 4 | 2.5 |
| 5 | 12.5 | 2.5 | 5.3 | 2.9 |
| 7.5 | 12.5 | 3.1 | 6.5 | 3.5 |
| 10 | 12.5 | 3.5 | 7.9 | 4.3 |
Table 4. Ablation volume at 12.5 joules and the rate of increase in the ablation volume.
| Time (min) | Power (Joules) | Volume (cm3) with a nickel-titanium alloy | Volume (cm3) with a gamma titanium | Rate of increase (cm3) |
|---|---|---|---|---|
| 1 | 15 | 0.5 | 4.9 | 4.3 |
| 2.5 | 15 | 1.4 | 6.2 | 4.7 |
| 5 | 15 | 2.6 | 7.5 | 5 |
| 7.5 | 15 | 3.3 | 8.8 | 5.7 |
| 10 | 15 | 3.6 | 10 | 6.3 |
Table 5. Ablation volume at 15 joules and the rate of increase in the ablation volume.
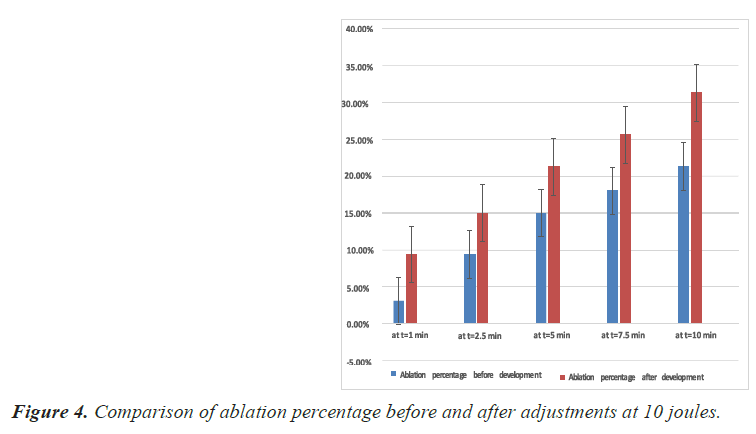
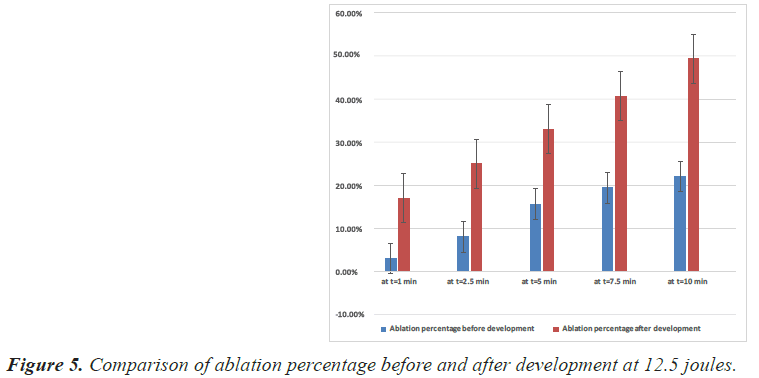
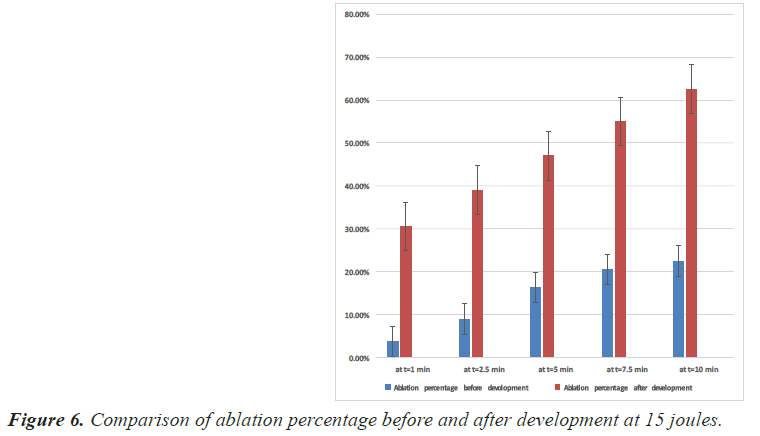
The simulation results and the percentage of ablation achieved before and after development at 10, 12.5 and 15 joules are shown in Figures 4-6 respectively.
It was shown from the results of the new design electrode after development
• At 10 joules: The maximum ablation volume increased from 3.4 cm3 to 5 cm3 and the ablation rate increased from 21.3% to 31.3% after ten minutes of ablation.
• At 12.5 joules: The maximum ablation volume increased from 3.5 cm3 to 7.9 cm3 and the ablation rate increased from 22% to 49.4% after ten minutes of ablation.
• At 15 joules: The maximum ablation volume increased from 3.6 cm3 to 10 cm3, and the ablation rate increased from 22.5% to 62.5% after ten minutes of ablation.
Conclusion
The results show that using gamma titanium instead of nickel-titanium achieved an increase in the ablation volume because it has higher electrical and thermal conductivity than nickel-titanium alloy. Also, the results show the effect of tuning parameters (ablation power, ablation time and design of the electrode) on increasing the ablation volume and decreasing the ablation time. The results show that the electrode design is the most important tuning parameter because with the change of design from the reference model to our developed model, the effect and success of the rest of the tunning parameters appeared. That helps to reduce the patient's pain and increase the accuracy. Future work can study the effect of a RF multi-hooks electrodes on large tumors by using the same tuning parameters and compare it with a RF cool-tip electrode.