ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2018) Volume 29, Issue 1
A novel technique to secure the acute myocardial infarcta images by the enhancement of privacy level
1Department of Computer Science and Engineering, Sathyabama University, Chennai, India
2Department of Information Technology, Sathyabama University, Chennai, India
- *Corresponding Author:
- Viji Mary A
Department of Computer Science and Engineering
Sathyabama University, India
Accepted date: August 20, 2016
DOI: 10.4066/biomedicalresearch.29-16-320
Visit for more related articles at Biomedical ResearchIn our day today world, millions of people are affected by Acute Myocardial Infarction (AMI) disease. The coronary arteries are blocked due to the accumulation of atherosclerosis substances. Such blocks are visualised through cardiovascular Magnetic Resonance Imaging (MRI) scanning. It is very important to secure this biomedical record to avoid misuse of the same. This protection of image is beneficial for the health care providers. This paper particularly considers the privacy of Acute Myocardial Infarction (AMI) images by a novel ‘project edge’ technique. It also takes into account the difficulties and the challenges of other existing perturbation techniques. Experiments are done and the results prove that the performance metrics of the ‘project edge’ technique are higher than the existing techniques.
Keywords
Acute myocardial infarcta, Privacy preserving data mining, Random projection, Data perturbation, Privacy level.
Introduction
Privacy is an essential part in various applications of data mining, which mostly considers the areas of forensics, health, financial, behavioural, and other sort of confidential data. They may occur due to the requirement to create user profiles, build models related to social network and to detect terrorism among others. For example, mining the data of a health care system may have the necessity to dissect clinical records and other medical transactions. But the underlying problem is that the privacy laws may be broken when such different data sets of different users are combined. It is unsafe to allow the health organizations to disclose the data even though the identifiers are deleted because the original information can be identified by the building of identification attacks for connecting different data set [1]. Thus arises the need for better techniques which pay attention for securing private information. It also preserves the statistical behaviour and characteristics which are necessary for data mining related applications. The approach, we discuss in this paper are defined in the following way: Assume there are N organizations A1; A2; …; AN, where every organization, AI contains a transaction database DBi. It is quite common that some statistics related features of the union of the databases 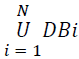 are required by the data miner. Though the organizations agree with the fact, they don’t like to outsource their actual information. It is very difficult for the third party user to analyse the data without balancing the privacy of such data. This is known as the census problem, which is illustrated by Chawla et al. [2]. At this point, the original data are generally perturbed and it is disclosed in its distorted form. Any user can access the released data. The work specifically takes into account a proposed technique to maintain privacy. This is boosted by the result furnished by Kargupta et al. in their research, which pinpoints the drawbacks of additive data perturbation [3]. In particular, the research work well discovers the chances of applying the technique of ‘project edge’ for building a modified form of data. The distorted data is revealed to the user who is mining the data. It can also be explained and proved that the statistical properties are maintained well in the distorted form of data. The theorem of Johnson and Lindenstrauss [4] laid the foundation for this approach which proves that a collection of points in a Euclidean space which is n-dimensional and can be mapped onto another subspace which is p-dimensional, where p=log n. Thus the pairwise length of the two points is secured by an atomic value. Hence, it is understood that the original information is susceptible to change when the data is mapped onto a lower subspace, while preserving its statistical characteristics. It is assumed that the confidential data is from the same domain and there is no sort of collusion between the parties.
are required by the data miner. Though the organizations agree with the fact, they don’t like to outsource their actual information. It is very difficult for the third party user to analyse the data without balancing the privacy of such data. This is known as the census problem, which is illustrated by Chawla et al. [2]. At this point, the original data are generally perturbed and it is disclosed in its distorted form. Any user can access the released data. The work specifically takes into account a proposed technique to maintain privacy. This is boosted by the result furnished by Kargupta et al. in their research, which pinpoints the drawbacks of additive data perturbation [3]. In particular, the research work well discovers the chances of applying the technique of ‘project edge’ for building a modified form of data. The distorted data is revealed to the user who is mining the data. It can also be explained and proved that the statistical properties are maintained well in the distorted form of data. The theorem of Johnson and Lindenstrauss [4] laid the foundation for this approach which proves that a collection of points in a Euclidean space which is n-dimensional and can be mapped onto another subspace which is p-dimensional, where p=log n. Thus the pairwise length of the two points is secured by an atomic value. Hence, it is understood that the original information is susceptible to change when the data is mapped onto a lower subspace, while preserving its statistical characteristics. It is assumed that the confidential data is from the same domain and there is no sort of collusion between the parties.
The summarization of the work is listed as follows. In Section 2, the literature survey of the existing distortion techniques is elaborately presented. The challenges of the existing techniques and the flaws of the other distortion techniques such as rule hiding, data swapping, k-Anonymity, random transformation, secure multiparty computation technique, random projection and morphological operations are discussed. Section 3 presents a proposed ‘project edge’ technique which will further increase the privacy and accuracy level of images. Experimental works and results are also provided to prove the efficiency of the proposed approach. Section 4 compares the hybrid ‘project edge’ technique with that of the existing distortion methods. The conclusion of the work is given in Section 5.
Related work
This section offers a concise survey of the related papers in the area of data mining to maintain privacy.
Data distortion techniques
Data distortion or perturbation methods are mostly categorized into the probability distribution and the perturbation of the value. In the first method, the actual data are either substituted by another data taken from the same set or substituted with the data set itself. The actual data are distorted by the addition or multiplication of noise, or by any other randomization algorithms in the value distortion method [5]. The existing data perturbation techniques to distort the data are translation, rotation, scaling and hybrid perturbation techniques. This work, specifically concentrates on the value distortion approach. It was the additive data perturbation technique that was proposed by Zhenmin et al. for the construction of decision tree classifiers [5]. It is referred to as a translation based perturbation technique and it is easily susceptible to attacks. Randomization is carried out for every item of the actual information by the addition of noise generated randomly which is selected from a distribution like a Gaussian. The original data is then reconstructed from its distorted form using algorithms like expectation maximization and then the categorization prototypes are built. Kargupta et al. queried his points on the addition of noise. He addressed that adding noise might compromise the privacy because of the fact that the additive noise can be withdrawn easily. The disadvantage of additive noise is overcome by the use of multiplicative noise for preserving the data privacy. There are two ways of introducing multiplicative noise [6,7]. One way is multiplying the element by a number which is spawned randomly. The number spawned randomly owns a Gaussian distribution which is a truncated one with a mean equal to one and a low variance level. The second one is choosing a log based conversion of the data and then to combine a Gaussian noise which is predefined as well as a multivariate one. Then the antilogarithm of the data is found out. In general, the first one is beneficial when the data distributor only needs to cause small modifications to the inaugural one. The latter approach offers greater privacy level, but the data utility is maintained in the logarithmic scale. The primary disadvantage of both the additive and multiplicative perturbations is that the pairwise similarity of data records is not preserved. This report proposes an alternate plan of attack that tests to maintain the average of statistical features of the information. The perturbation of data that occurs by adding or multiplying noise generally handles numerical data. In rotation based perturbation technique, each sub matrix is rotated independently and the properties of the data matrix were proved. The technique urges to generate perfect centralized procedures for mining data while protecting privacy. The limitation is that it can be applied only to the data split column wise. It cannot be applied to row wise partitioned data sets. The distortion of categorized data was studied first by Evfimievski et al. [8]. There was an evolution of a response method which is a randomized one to collect data via interviews. The distortion of categorical data was again taken into account, specifically in association rule mining which was proposed by Evfimevski et al. [9]. The work was stretched forth by Agrawal et al. by imparting in their framework, and a model for measuring the violation of privacy was brought into use [10]. The idea of γ amplification is used and is also applied in the model framework without the presumption on the subject of distribution. The actual information is taken from the same distribution. This model was reconsidered by Dalenius et al. and they had explained for setting the parameters efficiently for perturbation for reconstruction while preserving amplification [11].
K-anonymity model
The difficulty that an owner of the data needs to portion out a quantity of identifiable data by not revealing one’s individuality is considered by the k-anonymity technique. Suppression and data generalization are the techniques to overcome this problem. These techniques maintain the privacy related information. The best solution is to define all the quasiidentifiers which are used for connecting to data from external sources. The information is released only when the person’s data which is on the waiver could not be keyed out from k-1 persons.
Data swapping technique
Fienberg et al. [11] had initially recommended the fundamental principle of data interchanging, which is a modified version of the technique proposed by Dalenius et al. This idea is implemented by changing the data repository by exchanging some set of properties between the chosen set of tuples so that the data confidentiality is not disturbed. The marginal counts are also preserved. This technique can be categorized under data perturbation. Many modifications and applications of the data swapping technique are quoted in their proposed technique.
Secure multiparty computation (SMC) technique
This technique Secure Multiparty Computation (SMC) takes into account the difficulty of accessing a subroutine of the confidential inputs from more than one party in such a way that only the output of the function is revealed to the parties. The main building blocks of Secure Multiparty Computation (SMC) are the huge quantity of cryptographic protocols such as homomorphic and commutative encryption, circuit evaluation protocol and oblivious transfer. A detailed idea about Secure Multiparty Computation (SMC) framework along with its applications to the field of data mining is reported by Pinkas [12]. The work put forward by Goldreich offered a detailed introduction to Secure Multiparty Computation (SMC) [13]. It was explained clearly that any subroutine which is manifested by an arithmetic circuit can be calculated by means of an arbitrarily circuit assessing protocol. But, this will make the approach impracticable for huge datasets. A set of Secure Multiparty Computation (SMC) tools such as secure sum, inner product and set union beneficial for large-scale data privacy are briefed by Clifton et al. [14]. The techniques related to privacy preserving in data mining and its state of the art is explained clearly by Agrawal et al. [15].
Distributed data mining approach (DDM)
This Distributed Data Mining (DDM) approach helps to compute the prototypes of data mining and to extract certain “patterns” at a given connection point by interchanging very few data between the group of nodes that are taking part in [16,17]. Merugu et al. had proposed a paradigm for grouping distributed confidential data either in a semi supervised or in an unsupervised scenario [18]. An algorithm proposed by Gowri et al. show a novel method for the process of clustering in which the accuracy of clustering the data is described very appropriately, this algorithm would help in the process of pattern finding in the image. According to another algorithm, a model is built by each local site which transmits the model parameters to the global site. Here, it constructs a clustering model. An algorithmic procedure to maintain privacy for a Bayesian network model is briefed by Meng et al. [19].
Rule hiding
The principal target of this technique is to translate the data repository in order to hide the sensitive rules and the complete fundamental patterns can still be considered. It was formally proven by Atallah et al. that the best sanitization is an NP-hard problem to mask the confidential huge data sets in association rule mining [20]. Certain heuristic methods are used to overcome the difficulties. For example, the perturbation-based association rule hiding technique is adopted out by changing a selected set of 1-values to 0-values or vice versa, hence that the frequent item sets that generate the rule are handled or the relief of sensitive rules is taken down to a user-specified threshold [21]. Certain data attributes are replaced by a question mark in the blocking based association rule hiding approach [22]. In this regard, the minimum support and assurance will be modified into a minimal interval. The data sensitivity is needed to be saved or maintained until the support and/or the confidence of a confidential rule raises above the middle in the two areas.
Random orthogonal transformation
This part represents multiplicative distortion which uses orthogonal matrices generated randomly in the calculation of the inner product matrix. The deficiency of the applied method shall be analysed and a general case is suggested that uses random projection matrices to protect data in a better way. The transformation of an orthogonal transformation is linear T: ITn → ITn, which maintains both the size and the angles between the vectors [23].
Generally, orthogonal transformations can be represented by orthogonal matrices. Assume A and B are two data sets possessed by Vicky and Micky. Let A be an a1 × b matrix, and B is an a2 × b matrix. The same attributes are observed in both the data sets. Assume R as a random orthogonal matrix of size n × n. Let us now take the linear conversion of the data sets:
X=AR; Y=BR; → (1)
Then, XXT=AAT; YYT=BBT → (2)
XYT=ARRTBT=ABT → (3)
If the data owners Vicky and Micky outsource only the distorted version, it is possible to compute the pairwise angles and distances in between the row vectors. Hence, implementing a distance based data mining application for a horizontally partitioned data becomes very easy. In the same way, if the data is transformed such that, X=AR; Y=BR; then we have, XTY=ATB and the pairwise similarities are fully maintained in the disturbed data. Thus, a third person can examine the interconnection of the properties of column wise split data which is heterogeneously distributed without accessing the sensitive data. The observer cannot guess the actual form of the original data because there are a number of inputs and a lot of transformation probabilities. Hence, the random orthogonal transformation appears to protect data’s privacy in a more serious fashion, maintaining its utility. The transformation is called a ‘rotoinversion’ which is a rotation continued by a flip, when the value of the determinant is -1. Hence, the original data can be identified by means of a proper revolution. Figures 1a and 1b display the working of a random transformation in 3D orthogonally. The data are not perturbed well after random orthogonal transformation. Therefore, the technique of random rotation also does not secure the data up to the expected level [24].
Random projection
Basic mechanism: The technique of random projection projects an image of a higher dimensional plane to its subsequently lower-dimensional plane. The principle conception of random projection stems from the Johnson’s theorem which is briefed below:
Lemma 1: (Johnson-Lindenstrauss Lemma).
For an integer p and for ε, where 0< ε <1, if m is non-negative, then. For a set P of p= |P| data points in ITn, the mapping function is given by f: ITn → ITl, hence, for all a, b Є P, (1-ε) || a-b ||2 ≤ || f (a) – f (b) ||2 ≤ (1+ε) || a-b||2
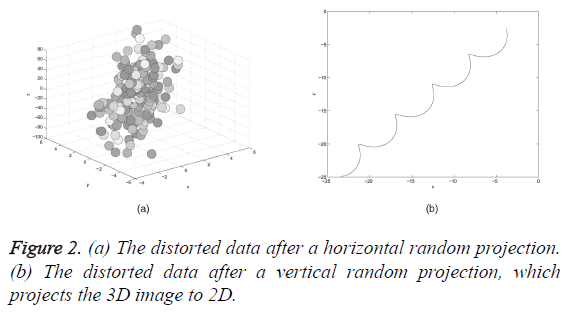
The lemma very clearly explains that a collection of p points in a k-dimensional expanse of Euclidean can be mapped onto a O (log p/ε2) dimensional expanse and hence the pairwise similarities of any two points are preserved by a small number. This wonderful characteristic infers that the data’s actual form can be changed by the reduction of its dimensionality yet still preserves its statistical properties. Both the horizontal and vertical projection of the input data is carried out. The input image is illustrated in Figure 1a. The resultant images are displayed in Figures 2a and 2b. From the result, it is seen clearly that the actual form of the data is disturbed and it is very hard to perceive. Other characteristics of the random projection technique and random matrices are discussed in the following which helps in preserving the data utility.
The original data is given in Figure 1a.
Lemma 2: Assume M as a × b matrix. Every element mij of M is independent and it is identically taken from a certain unknown distribution which has mean zero and variance as σ2m, then D [MT M] = a σ2m I and D [MMT] = b σ2m I.
Proof: Let mij and εij be the ith and jth entries of matrix M and MT M
![]()
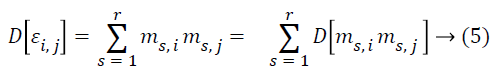
The random matrix entries are identically distributed and are independent and hence,
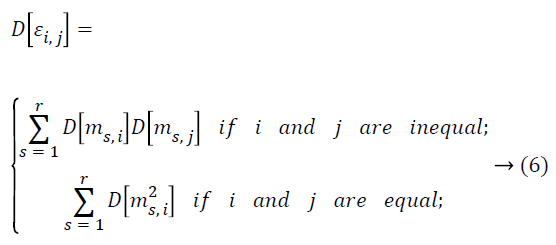
Also, it is noted that
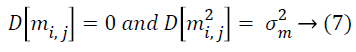
Hence,
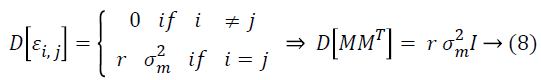
Identically, we have ![]()
The observation was already made that vectors which have random directions are mostly perpendicular in an mdimensional space where m is greater than or equal to 1. The random projection technique will be more powerful when it is combined with the other perturbation techniques.
(Projection by rows). Suppose Vicky and Micky are the owners of the data sets A and B respectively. Let A, B and C are the matrices where A=a × b1, B=a × b2 and C=k × a (k<a) be a random matrix. Every element ci, j of C is unrelated and it is exactly taken from a certain distribution which has mean=0 and variance=σ2m. Also, let
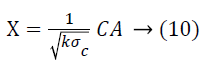
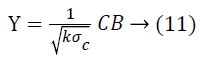
Then,
![]()
(Projection by columns). Suppose Vicky and Micky are the owners of the data sets A and B respectively. Let A, B and C are the matrices where A=a1 × b, A=a2 × b and C=b × k (k<b) be a random matrix. Every matrix element Ci, j of C is unrelated to each other and exactly taken from a certain distribution which has mean=0 and. Variance=σ2m Also, let
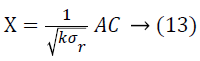
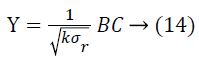
Then,
![]()
From the above results, it is absolutely clear that the horizontal projection maintains the inner product of columns and that the vertical projection maintains that of rows. Thus it is shown that the inner product is directly connected to many other distancerelated metrics. Some of them are:
The Euclidean distance of and b is given by the formula
![]()
The cosine angle of a and b, assuming that the data vectors are normalized to one.
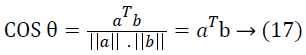
Suppose the data vectors are normalized to one with mean=0, then the correlation coefficient of a and b is
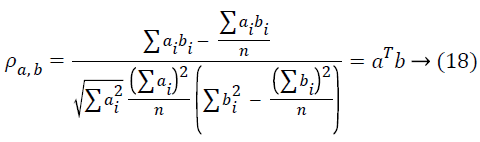
When the data attributes are decreased by means of projection, the statistical relationships will be saved. Similarly, if the observations are compressed, then the kinship between the attributes will really be saved. The mining procedures are applicable to the distorted data without disturbing the actual data. The drawback of random projection is it is highly unstable. Different projections result in different clustering results. The technique can be more powerful when it is combined with other perturbation technique.
Morphological operations
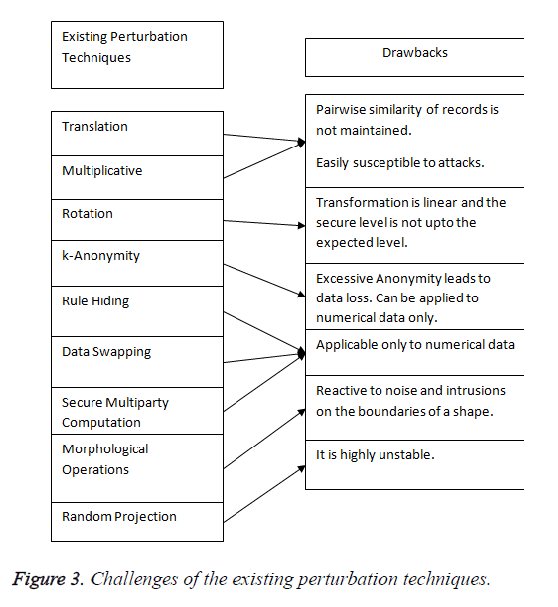
The morphological operations such as dilation and erosion, which changes the structure and shape of an image, also suffer from certain limitations. Sagar concluded that the basic morphological operations such as dilation and erosion are reactive to noise and obtrusions on the boundaries of a shape [25,26]. The operations will not produce better results if the objects are nearer with the distance (2* size of structuring element). The drawbacks of the existing perturbation techniques are illustrated diagrammatically in Figure 3.
Proposed ‘Project Edge’ Technique
The algorithmic steps of the proposed technique are given as follows.
Algorithm:
1). Input: An image A (a, b) and a matrix generated randomly C= (k<a) where k<a.
2). The input image A is projected into with and the perturbed form is
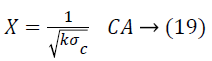
3). The boundary pixels of the image are detected using canny edge detection method.
4). Then the boundary pixel values of the perturbed image bab (X) are further distorted to Y=dab (X) in a nonlinear method.
5). The resultant image after doubly perturbed is Y.
6). The privacy level of the distorted image Y is calculated by the formula
![]()
Where Var represents the variance, A represents the actual image and Y the output image after perturbation.
7). The root mean square error value is also computed by
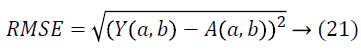
Discussions
The input image is perturbed twice. The size, dimensions and the original values of the input image are perturbed in step 2. Then the boundary pixels of the perturbed image are detected and again perturbed. The perturbation technique applied to the boundary pixels follows a nonlinear method. Hence, it is impossible to estimate the original form of data A and B, if the distorted data only is given. This is because the probability of finding out the solutions is infinite. Thus, it provides a very strong protection level of the image.
Experiments
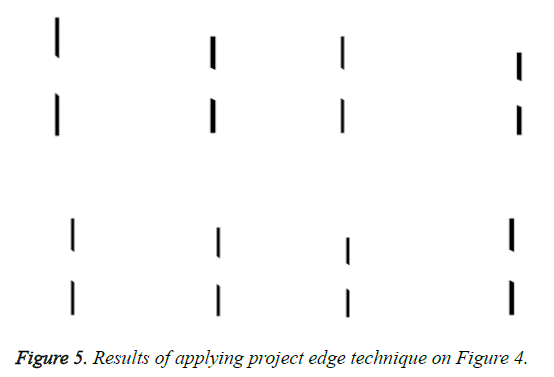
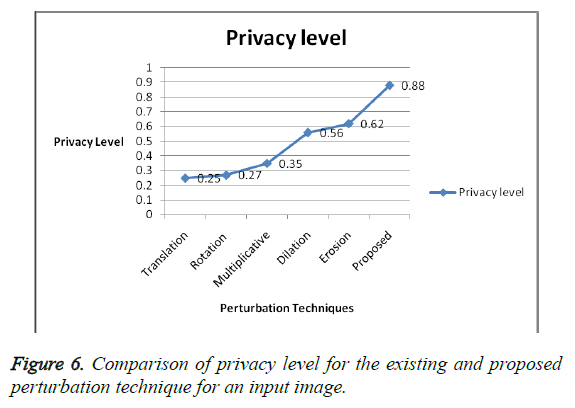
The shutter stock database is considered for the experimental work which is available in http://www.shutterstock.com/. Figure 4 shows a few sample medical images (AMI images) chosen from the database. 750 medical images of various dimensions are extracted from the database. Some of the sample images are displayed in Figure 4. The resultant images after the application of proposed project edge technique are shown in Figure 5. We also show in Table 1 that the proposed ‘Project edge’ technique increases the privacy level to a much greater level. The maximum privacy level hikes to 0.88. The accuracy of the image is also increased. This is proven by the computation of root mean square error values in Table 2. The lower Root Mean Square Error (RMSE) values represent a higher accuracy level. The average Root Mean Square Error (RMSE) value is 0.0024 which is very low and that accounts for higher accuracy.
| #Images | #Dimensions | Range of privacy level (0 to 1) |
|---|---|---|
| 250 | 2D | 0.80 - 0.86 |
| 200 | 3D | 0.75 - 0.85 |
| 200 | 4D | 0.76 - 0.87 |
| 100 | 5D | 0.82 - 0.88 |
Table 1: Privacy level of perturbed images of different dimensions.
| #Images | #Dimensions | Range of RMSE |
|---|---|---|
| 250 | 2D | 0.0015 - 0.0023 |
| 200 | 3D | 0.0013 - 0.0027 |
| 200 | 4D | 0.0016 - 0.0025 |
| 100 | 5D | 0.0020 - 0.0029 |
Table 2: Root Mean Square Error Value (RMSE) of perturbed images.
Comparison with Other Existing Techniques
The performance metrics of the proposed ‘project edge’ technique are compared with the other widely used techniques and the results are shown. Figures 6 and 7 present a comparison graph and chart of the privacy level and the root mean square error value with the existing techniques and the proposed technique. The privacy level of the existing techniques and the proposed technique are shown clearly in Figure 6 for an input image. The privacy level of the proposed technique is raised to “0.88” in the graph. The Root Mean Square Error (RMSE) value of the proposed technique is minimized to 0.0013. Thus the proposed technique possesses a maximum privacy level and a minimum Root Mean Square Error (RMSE) value compared to the existing perturbation techniques like translation, rotation, multiplicative, dilation and erosion. The graph and the bar chart in the Figures 6 and 7 depict a higher privacy level and accuracy level for the proposed technique compared to the existing techniques. A higher privacy level and a lower error value represent higher performance.
Conclusion
The proposed ‘project edge’ technique yields better results when compared with the other widely used existing techniques. This technique can be applied to images having dimension 2 and above. Higher performance is achieved by the proposed technique since it perturbs twice the original image. The image is collapsed dimensionally and the original form of data is impossible to detect if only the distorted data is given. The nonlinear technique is applied to modify the boundary pixel values after detecting the image boundaries. This in turn provides a stronger privacy level and the number of solutions to guess and find out the original image is infinite.
References
- Sweeney L. k-Anonymity: a model for protecting privacy. Intl J Uncertainty Fuzziness Knowl Sys 2002; 10: 557-570.
- Chawla S, Dwork C, McSherry F. Toward privacy in public databases. Proc Second Theory Cryptography Conf 2005.
- Kargupta H, Datta S, Wang Q, Sivakumar K. On the privacy preserving properties of random data perturbation techniques. Proc IEEE Intl Conf Data Mining 2003.
- Johnson WB, Lindenstrauss J. Extensions of lipshitz mapping into Hilbert space. Contemporary math 1984; 26: 189-206.
- Zhenmin Lin, Jie Wang, Jun Zhang. Generalized random rotation perturbation for vertically partitioned data sets. IEEE Symp Comp Intel Data Mining 2009.
- Agrawal R, Srikant R. Privacy preserving data mining. Proc Acm Sigmod Conf Manag Data 2000; 439-450.
- Kim JJ, Winkler WE. Multiplicative noise for masking continuous data. Statistical Research Division US Bureau of the Census 2003.
- Evfimievski A, Srikant R, Agrawal R, Gehrke J. Privacy preserving mining of association rules. Proc Eighth Acm Sigkdd Intl Conf Knowledge Discovery Data Mining 2002.
- Evfimevski A, Gehrke J, Srikant R. Limiting privacy breaches in privacy preserving data mining. Proc Acm Sigmod Pods conf 2003.
- Agrawal S, Haritsa JR. A framework for high-accuracy privacy-preserving Mining. Proc Intl Conf Data Eng 2005; 193-204.
- Fienberg SE, McIntyre J. Data swapping: variations on a theme by Dalenius and Reiss. Natl Inst Stat Sci Res 2004; 14-29.
- Pinkas. Cryptographic techniques for privacy preserving data mining. Sigkdd Exp 2002; 4: 12-19.
- Goldreich O. The foundations of cryptography. Cambridge Univ Press 2004; 2.
- Clifton, Kantarcioglu M, Vaidya J, Lin X, Zhu M. Tools for privacy preserving distributed data mining. Acm Sigkdd Exp 2003; 4.
- Verykios VS, Bertino E, Fovino IN, Provenza LP, Saygin Y, Theodoridis Y. State-of-the-art in privacy preserving data mining. Acm Sigmod Rec 2004; 3: 50-57.
- Park BH, Kargupta H. Distributed data mining. The handbook of data mining. Ser Human Fact Ergon 2003; 341-358.
- Liu KH, Ryan J, Bhaduri K. Distributed data mining bibliography, 2004.
- Merugu S, Ghosh J. Privacy-preserving distributed clustering using generative models. Proc IEEE Intl Conf Data Mining 2003; 211-218.
- Meng D, Sivakumar K, Kargupta H. Privacy sensitive Bayesian network parameter learning. Proc IEEE Intl Conf Data Mining 2004; 487-490.
- Atallah MJ, Bertino E, Elmagarmid AK, Ibrahim M, Verykios VS. Disclosure limitation of sensitive rules. Proc IEEE Knowl Data Eng 1999; 45-52.
- Verykios VS, Elmagarmid AK, Elisa B, Saygin Y, Elena D. Association rule hiding. IEEE Trans Knowl Data Eng 2004; 16: 434-447.
- Saygin Y, Verykios VS, Clifton C. Using unknowns to prevent discovery of association rules. Sigmod Rec 2001; 30: 45-54.
- Weisstein EW. Orthogonal transformation. Math W 2004.
- Kun L, Hillol K, Jessica R. Random projection-based multiplicative data perturbation for privacy preserving distributed data mining. IEEE Trans Knowl Data Eng 2006; 18 92-106.
- Sagar BT, Deepak K, Nirmal MD, Gopal P. Image Processing (IP) through erosion and dilation methods. Int J Emerg Technol Adv Eng 2013; 3 285-289.
- Raid AM, Khedr WM, El-dosuky MA, Mona A. Image restoration based on morphological operations. Int J Comp Sci Eng Info Technol 2014; 4 9-21.