ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 8
A hybrid neural network-gray wolf optimization algorithm for melanoma detection
1Department of Mathematics, University of Tafresh, Tafresh, Iran
2Department of Control Engineering, University of Tafresh, Tafresh, Iran
3Young Researchers and Elite club, Ardabil Branch, Islamic Azad University, Ardabil, Iran
- *Corresponding Author:
- Noradin Ghadimi
Young Researchers and Elite club Islamic
Azad University, Iran
Accepted date: November 12, 2016
Melanoma is one of the most dangerous tumors in the human kind cancers. Nonetheless, early detection of this cancer can help the doctors to cure it perfectly. In this paper, a new efficient method is proposed to detect the malignant melanoma images from the images. In the proposed method, a hybrid technique is utilized. We first eliminate the extra scales by using edge detection and smoothing. Afterwards, the main hybrid technique is applied to segment the cancer images. Finally by using the morphological operations, the extra information is eliminated and used to focus on the area which melanoma boundary potentially exists. Here, Gray Wolf Optimization algorithm is utilized to optimize an MLP neural Networks (ANN). Gray Wolf Optimization is a new evolutionary algorithm which recently introduced and has a good performance in some optimization problems. GWO is a derivative-free, Meta Heuristic algorithm, mimicking the ecological behaviour of colonizing weeds. Gray wolf optimization is a global search algorithm while gradient-based back propagation method is local search. In this proposed algorithm, Multi-Layer Perceptron Network (MLP) employs the problem's constraints and GWO algorithm tries to minimize the root mean square error. Experimental results show that the proposed method can develop the performance of the standard MLP algorithm significantly.
Keywords
Melanoma, Cancer, Tumors, Neural network
Introduction
In the recent years, human skin cancer is known as a major reason of deaths. Furthermore, because the skin has fine-scale geometry and complex surface, modelling of this phenomena is become a difficult case. Generally, the skin can be easily detected by eyes; however, there are many specific aspects of the skin which can better achieved by non-invasive imaging methods. The first step in achieving image characteristics for melanoma detection is to detect and localize the lesions in the image. Automated melanoma detection systems are based on using one imaging modality (like dermoscopy), computer algorithms and mathematical models to predict if a skin lesion is melanoma [1,2]. There are some different studies on this category which can be summarized in [2-4]. Back-propagation neural networks are one of the known classifiers which results good efficiency for segmenting the image classification problems. A significant drawback of the gradient descent technique is that Easy trapped in local minimum and slow convergence. In this paper to compensate this drawback, Gray Wolf Optimizer (GWO) has been used to find the optimal values for weights and biases in back-propagation algorithm. Because of its global searching feature, it can find optimal solutions in different directions in order to minimize the chance of trapped in local minimum and increment the convergence speed.
Filtering
In medical imaging, it is often desirable to perform some kind of noise and over-segmentation reduction on the considered image to ease the next processing steps. Median filter is a nonlinear digital filtering technique which is often employed to do this duty. This process is a typical pre-processing step to develop the results of later processing (in this paper detect of melanoma parts of an image. medical imaging keeps image edges under specific conditions while removing oversegmentation and noise (Figure 1). In case, the median filter replaces a pixel by the median of all pixels in its neighbourhood as below:
y [m, n]=median {x[i, j], (i, j) ϵ ω} → (1)
Here ω is a neighbourhood cantered around location (m, n) in the image [5]. Median filter considers the pixels in the image in turn and looks at their neighbours to make decision that is representative of its surroundings or not.
The utilized neighbourhood of the median filter depends on the image resolution. Here, 9 × 9 neighbourhood is used for images by the size of 256 × 256 pixels to show a complete melanoma.
Melanoma Supervised Classification
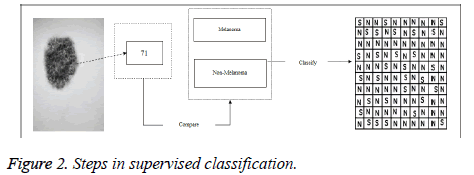
The main idea in the supervised classification in melanoma detection is to divide all the pixels of the input image into two classes (Melanoma and not melanoma classes); Figure 2 shows the steps of classification.
From the mathematics view, a neuron's network function f (x) can be described as a forming of other functions gi (x), which can be defined as other functions forming. This can be easily defined as a network structure, with arrows representing the dependencies between variables. A commonly used kind of forming is the nonlinear weighted sum, where
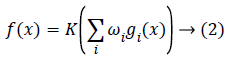
where K represents a predefined function, like the hyperbolic tangent. It will be easy for the following to assign a collection of functions gi as simply a vector g=(g1…gn). From different techniques, Back propagation (BP) is a commonly used method which is employed for feed forward networks. It evaluates the error on all of the training pairs and regulates the weights to fit the desired output. After training process, the network weights are ready to use for evaluating output values for new given samples. Neural network uses gradient descent algorithm to minimize error space. This algorithm has the drawback of trapping into the local minimum which is entirely dependent on initial (weight) settings. This objection can be removed by an algorithm by an exploration based algorithm, like the evolutionary algorithms.
Gray Wolf Optimizer
Gray Wolf Optimizer (GWO) algorithm is a new metaheuristic algorithm proposed by Seyedali et al. [6]. GWO is inspired from the hunting process of gray wolves in the wildlife. Wolves accustomed to live in a pack which divides into two gray wolves group: male and female for managing the other wolves in the pack. A too strong social overcome hierarchy is founded inside every pack. The social hierarchy of the pack can be organized as below:
1. The alphas wolves (α): The premier wolves in the cluster which are responsible for deciding. The alphas wolves orders are dictated to the cluster.
2. The betas wolves (β): the betas wolves comprise the second level among wolves cluster. The primary task of betas wolves is to support and backup alphas decisions.
3. The deltas wolves (δ): the deltas wolves are the third level wolves in the cluster which follow alpha and beta wolves. Delta wolves have 5 main groups.
4. The omegas wolves (ω): these wolves comprise the lowest levels in the cluster. They have to follow alpha, beta and delta wolves. Omegas wolves are the last wolves which are allowed to eat.
In GWO algorithm, the alpha (α) wolves are considered as the best solution of the objective while the second and third best solutions are belonging to the Beta (β) and delta (δ) wolves respectively. Here, the cluster is population and the solutions are belonging to omega (ω) wolves. Figure 3 shows the pseudocode of the gray wolf optimizer:
Figure 3: Pseudo code of the gray wolf optimizer [6]
ANN weights development using GWO (HNNGWO)
At first, ANN is trained using GWO algorithm to find the optimal initial weights. After that, the neural network is trained by using back-propagation algorithm which involves an optimal back-propagation network.
Check whether the network has achieved the considered error rate or the definite number of generations has been reached then to end the algorithm. For representing the ANN, a two layered network can be considered as follows:
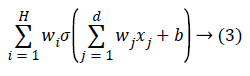
where H illustrates the number of neurons in the hidden layer, w is the network weights, b denotes value of the bias and σ is the activation function of each neuron which is considered as sigmoid in this case. The mean squared error of the network (MSE) can be defined as below:
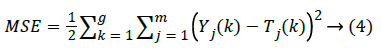
Here m is the number of nodes in the output, g is the number of training samples, Yj(k) defines the desired output, and Tj (k) is the real output.
The reason of the prominence of GWO against the EAs is that the EAs have been designed based on different mutation mechanisms. This mutation maintains the population diversity and develops the exploitation, which is one of the main reasons for the poor performance of ES. Furthermore, selection of individuals in these algorithms is performed by a deterministic approach. Since, the random selection in EAs is less and therefore local optima avoidance is less as well which makes the EAs to fail in providing good results in the datasets. In addition, the main reason for the high classification accuracy in the GWO-MLP algorithm is that this technique has adaptive parameters to smoothly balance exploitation and exploration as half of the iteration is employed to exploration and the others set to exploitation. The other advantage of GWO algorithm is that always saves the three best achieved solutions at any stage of optimization. A good comparison of the GWO against the other optimization algorithm can be obtained [7].
Simulation Results
The main database for testing the proposed method is extracted from Australian Cancer Database (ACD) [8,9]. In this paper two area for classification (as cancer and healthy) is considered. The proposed technique is based on pixel classification which classifies each pixel, independently from the neighbours. The input layer of the network comprises 3 neurons from each image either cancer or non-cancer image. Here, sigmoid function is used as the activation function of the MLP network. The output is between 0 and 255 (uint 8 class).
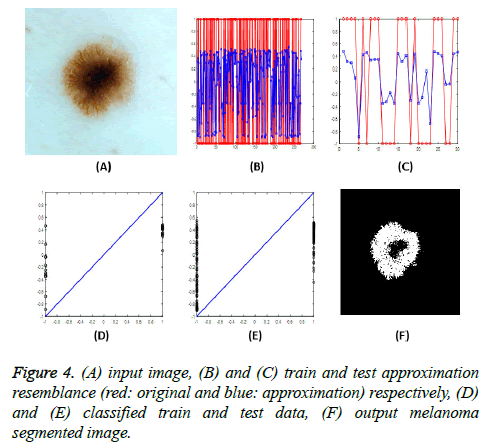
After applying the input image to the neural network and achieving the target output, a single threshold value is used to characterize the cancer and non-cancer pixels (Figure 4). For analyse the proposed method's efficiency, three performance metrics are introduced. Correct Detection Rate (CDR), False Acceptance Rate (FAR) and False Rejection Rate (FRR). The FAR and FRR are defined in Equations 7 and 8, respectively:



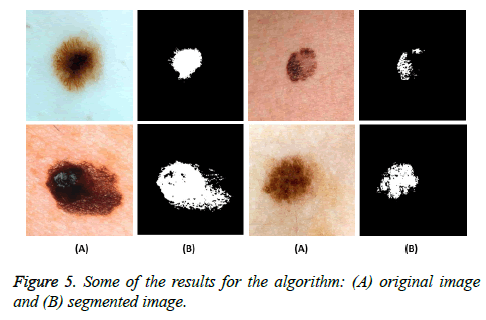
Figure 5 shows some examples of the input skin image and their output as the melanoma detected regions
We can see from the above results that the proposed algorithm has better efficiency in the accuracy. It is obvious from the above that the optimized MLP has better performance in both accuracy and time; Table 1 shows the final results. Finally, 90% accuracy for the best classifier is reached.
| Metric | Ordinary MLP | MLP-GWO |
|---|---|---|
| CDR (%) | 88 | 90 |
| FAR (%) | 7.5 | 6.5 |
| FRR (%) | 4.5 | 3.5 |
Table 1. Classification comparison of performance in the proposed method.
Conclusion
In this paper, an automatic method for segmenting the melanoma cancer images is proposed. The proposed method is a new hybrid algorithm between artificial neural network and gray wolf optimizer for enhancing the back-propagation algorithm efficiency and for escaping from trapping in the local minima. The high level of exploration and exploitation of gray wolf optimizer were the motivations for this study. Simulation results showed that GWO helps ANN to find the optimal initial weights and to speed up the convergence speed and reduce the RMSE error. To compare the performance of the proposed method by the ordinary ANN, three metrics (CDR, FAR and FRR) are employed and the results show good efficiency for the proposed ANNGSA algorithm toward ordinary ANN (Table 1).
References
- Razmjooy N, Musavi BBS, Soleymani F. A computer-aided diagnosis system for malignant melanomas. Neural Comput Appl 2013; 23: 2059-2071.
- Ganster H, Pinz A, Rohrer R, Wildling E, Binder M, Kittler H. Automated melanoma recognition. IEEE Trans Med Imaging 2001; 20: 233-239.
- Xu L, Jackowski M, Goshtasby A, Roseman D, Bines S, Yu C, Dhawan A, Huntley A. Segmentation of skin cancer images. Image Vision Comput 1999; 17: 65-74.
- Ganster H, Pinz A, Rohrer R, Wildling E, Binder M, Kittler H. Automated Melanoma Recognition. IEEE Transact Med Imaging 2001; 20: 233-239.
- Razmjooy N, Mousavi SBB, Soleymani F. A real-time mathematical computer method for potato inspection using machine vision. Comput Math Appl 2012; 63: 268-279.
- Seyedali M. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl Intel 2015; 43: 150-161.
- Celebi ME, Aslandogan YA, Bergstresser PR. Mining biomedical images with density-based clustering. Int Confer Inform Technol: Coding and Computing, IEEE, 2005.
- http://www.aihw.gov.au/australian-cancer-database/
- Guha D, Roy PK, Banerjee S. Load frequency control of interconnected power system using grey wolf optimization. Swarm Evolution Comput 2016; 27: 97-115.