ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2019) Volume 30, Issue 5
A comparison of the time homogeneous and time non-homogeneous markov models for monitoring HIV/AIDS disease progression: Results from patients on ART.
Claris Shoko1*, Delson Chikobvu1, Pascal O. Bessong2
1Department of Mathematical Statistics and Actuarial Sciences, University of the Free State, Bloemfontein, South Africa
2HIV/AIDS & Global Health Research Programme, University of Venda, Thohoyandou 0950, South Africa
Accepted Date: April 03, 2019
DOI: 10.35841/biomedicalresearch.30-19-142
Visit for more related articles at Biomedical ResearchBackground: Markov models are widely used in studying progression of chronic diseases using the time homogeneity approach. Relatively few studies use the time non-homogeneous approach to model the progression of HIV/AIDS based particularly in the use of viral load monitoring mainly due to fact that that viral load is expensive to measure frequently hence not readily available in the format required. Non-homogeneous models reveal the interval in which viral rebound occurs. Methods: This study compares the time-homogeneous Markov approach to the time nonhomogeneous approach in predicting HIV/AIDS progression. A piece-wise constant approach to non-homogeneous modelling is used. Results: This study reveals that a piece-wise constant Markov approach to non-homogeneous modelling which allows variation in transition rates within intervals [0,0.5) years and [0.5,∞) years is better for predicting HIV/AIDS progression compared to the time-homogeneous approach. Failure to combination antiretroviral therapy (cART) increases significantly the rate of viral rebound and deaths 6 months post treatment initiation. Conclusion: Hence, there is need to closely monitor the uptake of antiretroviral drugs in the first six months of treatment to increase the chances of survival for HIV/AIDS patients.
Keywords
Non-homogeneous Markov model, Time-homogeneous Markov model, HIV/AIDS progression, Viral load.
Introduction
Combination antiretroviral therapy (cART) reduces HIV viral load by blocking replication of the virus [1-3]. Hence, constant monitoring of viral load counts is beneficial over routine monitoring of CD4+ cell count since immunodeficiency can be prevented by early detection of virologic failure thereby enabling proper management of HIV/AIDS patients by interested stakeholders [4].
The suppression of HIV viral load from very high levels, greater than 500 000 copies/mL, to suppressed levels due to the effects of cART can be considered as a multi-state process based on the viral load including the endpoint, death state. Patients are then monitored only at visit times resulting in the exact time the transition occurred to be unknown [5]. Homogeneous and non-homogeneous Markov processes are an important field of research when dealing with interval censored data in which the exact time of transition is not known. A Markov process is a stochastic process in which the probability of transition to a future state given the current state is independent of the past history. Thus, a Markov model possesses the memoryless property involving random movements between states that occur at regular or irregular intervals [6].
The constant hazard assumption of the time-homogeneous models is unrealistic when modelling evolution in chronic diseases [7] because they put severe limitations on the previous behaviour of the disease [8]. However, most applications to HIV/AIDS disease assumed a homogeneous process where transition probabilities only depend on the elapsed time between observations [6,9-11].
Application of non-homogeneous Markov models to study the evolution of HIV allows computations of estimates of the time in which HIV patients spend in each state but also the randomness of different states in which the states can evolve known as a stochastic process [12]. Saint-Pierre et al. used a piece-wise approach to non-homogeneous Markov modelling on asthma patients. They argued that piece-wise constant transition intensities help in preserving the tractability of constant intensities [8]. However, non-homogeneity is not treated in survival analysis as extensively as homogeneous models and in particular for HIV/AIDS disease progression when based on viral load monitoring [13].
This paper models the virology of HIV using a piece-wise constant approach to form a time non-homogeneous Markov process. The virology of HIV is split into mutually exclusive states defined by viral load including the absorbing state, death. The use of Markov models with piece-wise constant transition intensities helps in preserving the tractability of constant intensities [8].
In the next section we describe the HIV/AIDS data that is used in this study and also how the model is formulated basing on the data. In section 3, we have results and analysis where three different models are fitted and their appropriateness is assessed using the Akaike Information Criteria (AIC), likelihood ratio tests as well as the plots of percentage prevalence in each state. The last section discusses and concludes the findings.
Materials and Methods
Data description
The data set used in this study has been described in previous studies [14-17]. At treatment initiation the variables age, Viral Load Baseline (VLBL) and CD4 baseline (CD4BL) are described in Table 1.
| Variables | Age (years) | VLBL (copies/µL) | CD4BL (copies/mm3) |
|---|---|---|---|
| Minimum | 15 | <50 (undetectable) | 16 |
| First Quartile | 32 | 21 334 | 38 |
| Median | 39 | 67 995 | 116 |
| Mean | 40.62 | 138208 | 156 |
| Third Quartile | 47 | 201 445 | 206 |
| Maximum | 77 | >500 000 | 1202 |
Table 1: Descriptive Statistics for variables age, baseline viral load and baseline CD4+ cell count.
For each and every visit, blood samples were obtained for each patient and stored frozen until assayed. Plasma HIV RNA was measured using an amplicator HIV-1 monitor assay kit which has a limit of sensitivity ranging from 50 copies/μL to 500 000 copies/μL.
Table 2 shows the possible transitions between the defined states from t=0 to t=1.5 years of treatment uptake.
| Variables | Viral load States | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| t=0 years | 4 | 43 | 134 | 106 | 32 | 0 |
| t=0.25 years | 155 | 123 | 6 | 4 | 4 | 24 |
| t=0.5years | 214 | 48 | 13 | 2 | 3 | 11 |
Table 2: Number of HIV/AIDS patients in each viral load state from t=0 to t=0.5 years.
At enrolment, most patients were in state 3 followed by state 4. State 1 had the least number of patients but during the first 0.25 years, it had the highest number of patients followed by state 2. From t=0.25 to t=0.5 years, the number of patients in state 3 increased from 6 to 13, an indication of viral rebound since the number of patients with higher viral loads (state 3 and state 4) reduced collectively only by 3. There is need to investigate the causes of viral rebound for HIV/AIDS patients since they are on treatment.
Model formulation
The non-homogeneous continuous time Markov model is formulated by splitting HIV/AIDS progression into 5 viral load defined states followed by the end point, death, which is state 6. The HIV/AIDS progression states are:
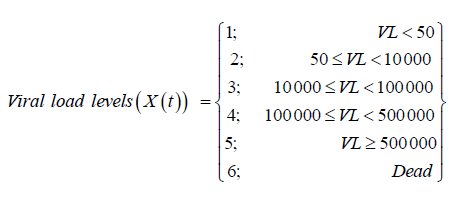
These 6 states define the HIV/ AIDS disease process is denoted by X (t) as shown above. The machine that is used to detect the viral load used thresholds of [50; 500 000) such that viral load below 50 copies /mL is classified as undetectable. The other covariates included in the model are.
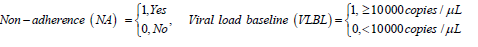
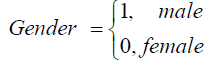
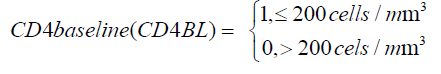
Formulation of the model is based on the approach by Saint- Pierre and others [8] where the study period [τ_(l-1),τ_l) for, l=1,….,r+1, and considering a vector of artificial timevarying covariates
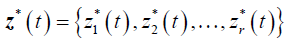
such that:
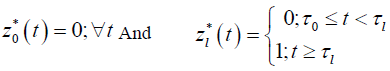 for
for
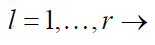 (1)
(1)
And the model with transition intensities;
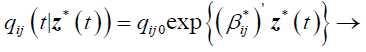 (2)
(2)
qij0 is the baseline transition intensity corresponding to the interval [τ0,τ1], β*ij is a vector of regression coefficients associated with the artificial time-varying covariates. For this model the transition intensities are step-functions of time defined for each interval as follows:
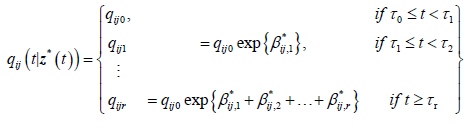
Incorporating the effects of covariates, the model becomes
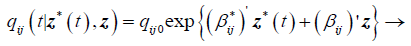 (3)
(3)
Where qij0 is the baseline transition intensities for the interval 0 ≤ t<0.5 with covariates set to their means, r is the log-linear effect of the r interval on the baseline transition intensity and Z*t is the artificial time-dependent covariate, βij is the log-linear effect of the relating the instantaneous rate of transitions from state i to state j to the covariates
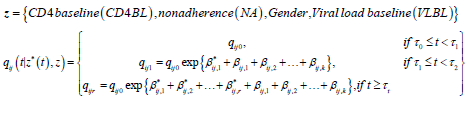
Statistical analysis
All the analysis is done using the Multi-State Modelling [MSM] package for multistate modelling in R software developed by Jackson [18]. The process of identifying the appropriate model started off by fitting time homogeneous Markov model for the data. The time homogeneous model converges and has -2Log-likelihood of 2799.465. From this time homogeneous model, percentage in each state are estimated and plotted as shown in Figure 1.
A comparison of the expected prevalence and observed percentages in each state from Figure 1 show that the predicted number of HIV infected individuals who die (State 6) is underestimated by the model from about 1 year onwards. The number of individuals alive and in state 1 is overestimated by the model from 1 year onwards. Such discrepancies, according to Jackson, indicate a possibility that the transition rates vary with time since the beginning of the process. In this particular case, it could be the time on treatment therapy [19,20]. This calls for the need to fit a Markov process that is non-homogeneous which can be handled by fitting a piecewise constant function.
Individuals in this study were followed up after every 6 months, thus we start off with a 9-segment non-homogeneous Markov model with 0.5 year intervals. Although the 9-segment model did not converge to maximum likelihood, the prevalence plots for each state in the model helped in revealing intervals with constant transition intensities.
We further investigated the best piece-wise constant function for the data by considering different change points. Most of the models did not converge to a maximum likelihood except for the models;
1. With 2-segments and having a change point at 0.5 years.
2. With 2-segments and having a change point at 1 year.
3. With 3-segments and having change points at 0.5 and 1 year.
In the next section, we base our analysis on these three models and also the time homogeneous model. We further investigate the effects of covariates; gender, non-adherence and CD4 baseline on the chosen model.
Results
For the 2-segment model, the transition intensities are defined for the following intervals.
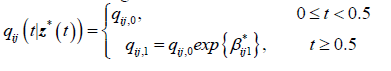
Where qij,0 is the baseline transition and qij,1 is the transition intensity matrix for the interval t ≥ 0.5years and β*ij1 is the regression coefficient associated with the artificial timedependent covariate Z1 *(t). The point estimates of parameters and their corresponding confidence intervals are shown in Table 3.
| Variables | Baseline [qij,o]Â |
Log-linear effect [βij1]Â |
Hazard Ratios  [0.5,Inf) |
|---|---|---|---|
| q12 | 0.445 (0.360, 0.550) | -1.295 (-1.814, -0.777)* | 0.274 (0.163,0.460) |
| q16 | 0.053 (0.031, 0.091) | -3.170 (-4.011, -2.330)* | 0.041 (0.018,0.097) |
| q21 | 2.640 (2.244, 3.107) | -1.133 (-1.426,-0.841) * | 0.322 (0.240,0.431) |
| q23 | 1.585 (0. 486, 5.168) | -2.660 (-6.353, 1.033) | 0.070 (0.0017, 2.810) |
| q26 | 0.002 (0.0000003742, 727) | 1.220 (-25.055, 27.495) | 3.387 (0.0000000013,870000000) |
| q32 | 6.635 (2.158, 20.40) | -3.854 (-7.347, -0.361)* | 0.021 (0.0006,0.697) |
| q34 | 6.110 (0.015, 2428) | 3.010 (-5.893, 11.91) | 20.28 (0.0028,149100) |
| q36 | 0.144 (0.0018, 11.64) | 4.071 (-8.064, 16.21) | 58.63 (0.0003,11000000) |
| q43 | 47.116 (0.137, 16160) | 1.387 (-7.123, 9.897) | 4.004 (0.0008,19870) |
| q45 | 3.772 (0.010, 1356) | -0.849 (-9.605, 7.907) | 0.428 (0.000067,2717) |
| q46 | 0.02 (0.0000000000, 680000000000) |
2.426 (-194.2,199.1) | 11.316 (0.0000000000046,28000000000) |
| q54 | 23.825 (0.089, 6378) | 0.649 (-7.528, 8.825) | 1.913 (0.0005,6804) |
| q56 | 0.035 (0.0000000013, 934000) | 2.707 (-26.46, 31.87) | 14.99 (0.00000000032,6950000000) |
| -2xLL | 2495.898 | ||
Table 3: Baseline transition intensities for the 2-segment non-homogeneous model and the time varying log-linear effects.
The results from Table 3 also narrow confidence intervals for transitions from state 1 and from state 2 except for the transition from state 2 to 6 (death). This shows that estimates of transitions from these states are statistically significant. However, most of the point estimates have wide confidence intervals and therefore are not statistically significant. This could be due to the fact that within 6 months of treatment uptake, most patients had made transitions to either state 1 or state 2 as shown by the prevalence plots in Figure 1.
Next we compute estimates of parameters for the 3-segment non-homogeneous Markov model with half-year and oneyear change points, with transition intensities defined for each interval as follows:
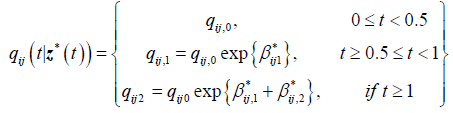
is the baseline transition intensities for the interval, 0 ≤ t <0.5, β*ijr tis the log-linear effect of the rth interval on the baseline transition intensity and Z*(t) is the artificial time-dependent covariate. The estimated parameters are shown in Table 4.
| Variables | Hazard Ratios | Log-linear Effects [βij] | |||
|---|---|---|---|---|---|
| No. | Baseline [qij,o]Â | [0.5,1) | [1,Inf) | ||
| q12 | 0.441 (0.357, 0.546) |
0.393 (0.198,0.781) | 0.246 (0.145,0.419) | -0.933 (-1.619,-0.248)* |
-1.401 (-1.932, -0.870)* |
| q16 | 0.0572 (0.0349, 0.0937) |
0.0396 (0.0067,0.233) | 0.0482 (0.0209,0.111) | -3.230 (-5.002,-1.458)* |
-3.032 (-3.866, -2.198)* |
| q21 | 2.607 (2.208, 3.079) |
0.447 (0.275,0.725) |
0.289 (0.210,0.400) | -0.806 (-1.289,-0.321)* |
-1.240 (-1.562, -0.917)* |
| q23 | 1.588 (0.501, 5.036) |
0.0836 (0.00205,3.404) | 0.0692 (0.00189,2.540) | -2.482 (-6.188, 1.225) |
-2.670 (-6.273, 0.932) |
| q26 | 0.00138 (0.00084, 2.268) |
0.293 (0.0484,1.773) | 2.111 (0.653,6.827) | -1.227 (-83.617,81.163) |
0.747 (-34.965, 36.460) |
| q32 | 6.775 (2.264, 10.027) |
0.0342 (0.0104,1.120) | 0.0203 (0.0067,0.61) | -3.376 (-6.866, 0.114) |
-3.900 (-7.306, -0.493)* |
| q34 | 4.832 (3.571, 6.540) |
4.364 (3.462,13.487) | 20.097 (2.418, 26.70) |
1.474 (-2.907, 5.854) |
3.001 (-6.025, 12.026) |
| q36 | 0.0585 (0.0108, 3.182) |
0.79946 (0.402,1.589) | 61.1451 (60.93,61.36) | -0.224 (-35.450,35.002) |
4.113 (-9.706, 17.932) |
| q43 | 36.307 (2.900, 45.46) |
0.688 (0.0691,6.851) | 3.951 (0.653,23.91) | -0.374 (-4.975, 4.227) |
1.374 (-7.334, 10.082) |
| q45 | 0.638 (0.165, 2.467) |
0.754 (0.518,10.96) | 0.0174 (0.0028,1.084) | -0.282 (-2.959, 2.395) |
-4.054 (-5.820, 7.712) |
| q46 | 0.00965 (0.00183, 5.081) |
2.063 (0.345,12.35) | 5.745 (0.997,33.12) | 0.724 (-74.748,76.196) |
1.748 (-214.14,217.64) |
| q54 | 26.276 ( 18.65, 37.02) |
0.0899 (0.0474,1.703) |
5.151 (3.504,7.572) | -2.409 (-5.35, 0.533) |
1.639 (-24.07, 27.353) |
| q56 | 0.0464 ( 0.0109, 1.960) |
180.816 (3.766,868.2) | 2.298 (0.00019,27.51) | 5.198 (-5.582,15.976) |
0.832 (-98.36,100.02) |
| -2xLL | 2485.745 | ||||
Table 4: Effects of half-year and one-year changes in time on the baseline transition
Results from Table 4 show an improvement on the estimated parameter values. This is shown by the confidence intervals that are narrower compared to the confidence intervals shown in Table 3 for the 2-segment model. However, transitions to death from states 2, 3, 4 and 5 have got very wide confidence interval. Only mortality rates from state 1 (undetectable viral load) decrease significantly with time as indicated by the narrow confidence intervals and exclusion of zero in the confidence intervals.
Next we present the results from a 2-segment piece-wise Markov model together with the effects of covariates. The model is given as follows:
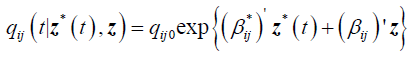
qij0 is the baseline transition intensities for the interval 0 ≤ t <0.5 with covariates set to their means, β*ijk is the log-linear effect of the kth interval on the baseline transition intensity and Z*(t) is the artificial time-dependent covariate, β*ij is the log-linear effect of the relating the instantaneous rate of transitions from state i to state j to the covariates.
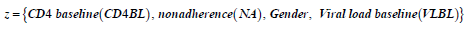
The results are shown in Table 5.
The results from Table 5 show that during the first 0.5 years of treatment uptake (baseline) the rates of viral load suppression are higher than the rates of viral rebound regardless of the state. The highest transition rates are noted from a viral load above 500 000 copies/μL to a viral load between 100 000 and 499 999 copies/μL. During the first six months most transitions to death occurred from a viral load state between 100 000 and 500 000 copies/μL. This is mainly attributed to initiating treatment with a CD4 baseline below 200 cells/ m^3.
Having a CD4 baseline below 200 cells/m^3 at treatment initiation contribute significantly to the increase in viral suppression to undetectable level as shown by a narrow confidence interval and exclusion of zero in the confidence interval. For these patients, there is also a significant increase in viral suppression from state 4 to state 3. Though not significant, there is reduction in viral suppression from state 3 to state 2.
For non-adherent patients, the results reveal a significant reduction in viral suppression to undetectable levels (state 2 to state 1). Thus, adherence to treatment increases significantly the transition rates to undetectable levels. Non-adherence increases transitions to viral rebound from undetectable viral load (state 1 to state 2). Although some of the estimated parameters are not significant, the results show that nonadherence to treatment contribute more to the increased rates of viral rebound than viral suppression.
Males in the study experience a reduction in the rates of viral suppression to undetectable levels, but once the undetectable viral load is reached they have reduced rates of viral rebound. This means that for their female counterparts, rates of viral suppression to undetectable levels are higher than that of males. Deaths of males are more likely to occur from viral load states between 10 000 and 500 000 copies/μL compared to their female counterparts.
The results also show reduction in the rates of transition to better states (viral suppression) for patients who initiated treatment with a viral load level above 10 000 copies/μL. These patients experienced increased transitions to death regardless of the viral load state. Thus, starting treatment with a viral load above 10 000 copies/μL increases the mortality rates and also accelerates diseases progression.
From 6 months (0.5 years) of treatment uptake onwards, most of the transitions between live states are significant except for the transition from state 3 to state 4 and state 5 to state 4. The results show a significant reduction in viral suppression to undetectable levels from 6 months onwards but once the undetectable viral load is reached there is reduction in viral rebound and also reduction in death occurrences. However, if the viral load is still detectable after 6 months, it increases the occurrence of deaths.
Assessment of the fitted models
In this subsection, we assess the fitted models using several techniques: prevalence plots, contour plots and estimates of log-likelihoods and Akaikie Information Criteria (AIC). Prevalence plots give a rough indication of the goodness of the fitted models and contours plot the likelihood surface with respect to 2 parameters default to plus or minus 2 standard errors obtained from the Hessian matrix at the maximum likelihood estimate.
In Figure 2 we compare the percentage prevalence plots for each of the states for the a two-segment non-homogeneous Markov model with change point at 0.5 years, 3-segment non-homogeneous Markov model and the 2-segment model with change point at 1 year respectively.
Results from the percentage prevalence plots show that the fitted model gives a perfect fit of the observed data for patients in state 2,3,4 and 5. However, the expected percentage prevalence plot for the 2-segment non-homogeneous model with change point at 1 year overestimates the observed plot for patients in state 1. From 3 years onwards, expected percentage prevalence for mortality (state 6) underestimate the observed mortality from all fitted models although the 2-segment model with change point at 1 year underestimates mortality from 2 years onwards. Compared to the prevalence plot for the time homogeneous model shown in Figure 1, these plots show an improved fit to the observed data.
The prevalence of State 1 is down sloping from half a year on. This is due to non-adherence to treatment as shown by the results in Table 4.
Before computing estimates of AICs we plot the contours for the fitted models. These contours help to diagnose any irregularities in the likelihood surface. Thus, they present a graphical visualisation of the fitted surface. For biological data, these contours are expected to be elliptical. Figure 3 shows contours for the fitted models.
Figure 3 shows that contours for the time homogeneous Markov (top left) are not elliptical but the contour for the three non-homogeneous models are elliptical. So the nonhomogeneous model give a better fit the data compared to the homogeneous model. However, the contours for the time homogeneous model (top left) and the contours for the 2-segment with change point at 1 year (top right) are not symmetric; hence the models cannot explain this data fully. The contours for the non-homogeneous models; 2-segment with change point at 0.5 years (bottom left) and 3-segment with change points at 0.5 and 1 year (bottom right) are both elliptical and evenly distributed contours plots with symmetrical surfaces that peak at the centre (indicated by the white region). Hence these models give an adequate explanation of the data.
Table 6 shows estimates of the -2xlog-likelihood (-2 × LL), log-likelihoods (LL) are shown in brackets, the degrees of freedom for each of the fitted models and the Akaike information criteria (AIC). The AICs are calculated using the
formula;
AIC = −2log(likelihood) + 2× df
For example, for the homogeneous model AIC=2799.465+2x13=2825.465 as shown in the Table 6.
The results show that the time homogeneous Markov model has the highest AIC and log-likelihood compared to the non-homogeneous Markov models. From the fitted non-homogeneous Markov model, the 3-segment model, with change points at 0.5 and 1 year, has the highest loglikelihood compared to all the other fitted models followed by the 2-segment model with change points at 0.5 years. However, a further assessment basing on the AICs reveal that a 2-segment model with change points at 0.5 years fits the data better than the 3-segment model since it has the lowest AIC. Effects of the covariates were included in the 2-segment non-homogeneous model and the model yielded the lowest AIC.
Discussion
In this study, a comparison of the time-homogeneous Markov model and the non-homogeneous Markov model to estimate the progression of HIV/AIDS on viral load monitoring is done. For this model, the expected percentages in state 1 overestimated the observed percentages and the predicted number of individuals who died was underestimated by the model from 1 year of treatment uptake onwards. This indicated the need to fit a non-homogeneous model in which transition intensities are piece-wise constant. Nonhomogeneous models with different change points were fitted. However, most of these models did not converge to a maximum likelihood except for the 2-segment model with change point at 0.5 years, 2-segment model with change point at 1 year and 3-segment model with change points at 0.5 and 1 year. From these models, non-homogeneous models and the time homogeneous model, assessment of the best model was done using the percentage prevalence plots, contour plots, perspective plots, CIs, log-likelihoods and the AICs. The model with the lowest AIC, the 2-segment model with change point at 0.5 years, was considered as the model that best explains HIV progression in patient on treatment under viral load monitoring for this data set.
This means that HIV progression is best described by a non-homogeneous Markov model with a change point at 0.5 years. This is mainly influenced by the results from viral load monitoring which are that, most of the patients on antiretroviral therapy reach the undetectable viral load within the first six months of treatment uptake (14,16). Thus, when monitoring HIV/AIDS patients, one should ensure that viral load suppression is reached as this reduces mortality rates.
Results from the fitted models show wider confidence intervals for the estimated transition rates to death. However, transitions within the 5 live states defined by viral load had narrow confidence intervals indicating significance in the estimated parameters, particularly the 2-segment model with change point at 0.5 years and covariates, in predicting transitions between live states.
The results also revealed a slower response to treatment when patients start treatment when viral load levels are above 10 000 copies/μL than when treatment is initiated when the viral load levels are below 10 000 copies/μL in the first 6 months [17]. Patients who initiated therapy with a viral load level above 10 000 copies/μL experienced accelerated rates of transition to death [14]. In 2018, Shoko et al. observed the same finding although they used a time homogeneous Markov modelling approach [17].
The results from this study revealed reduction with time in viral suppression to undetectable levels for males and patients who were non-adherent to treatment [14]. For males, once the undetectable viral load is reached, there is reduction in viral rebound particularly from 0.5 years onwards.
This study shows a significant reduction in transitions to death from 0.5 years onwards for patients who have achieved an undetectable viral load despite the challenges of nonadherence. Thus, time non-homogeneity is the best approach to modelling HIV/AIDS progression for patients receiving cART.
Ethics and Consent to Participate
The procedures used in this study were as approved by the Research Ethics Committee of the University of Venda, South Africa (Protocol number SMNS/13/MBY/01/0625), in accordance with the 1964 Helsinki declaration and its subsequent amendments. Additionally, permission to access health facilities was obtained from the Limpopo Provincial Department of Health, South Africa, and the collaborating health facilities. Informed consent was obtained from study participants prior to their involvement; and data obtained was stripped of personal identifiers to ensure the confidentiality of the participants.
Funding
The dataset used was generated from funding awards to POB by the South African Medical Research Council (RCDI) through funding received from the South African National Treasury, the South African National Research Foundation (GUN109312), and the University of Venda. The contents are solely the responsibility of the authors and do not necessarily represent the official views of the South African Medical Research Council , the National Research Foundation, or the University of Venda.
Availability of Data and Materials
The data is available upon a submitted request.
Author Contributions
CS drafted the manuscript. POB provided the data used for the analysis. CS, DC and POB contributed to the analysis and interpretation of the data. All authors participated in critical revision of the manuscript drafts and approved the final version.
Competing Interests
The authors declare that they have no competing interests.
Consent for Publication
Not applicable.
References
- Brennan AT, Maskew M, Sanne I, Fox MP. The Interplay between CD4 Cell Count, Viral Load Suppression and Duration of Antiretroviral Therapy on Mortality in a Resource-Limited Setting. Trop Med Int Health 2013; 18: 619-631.
- Cohen MS, Chen YQ, McCauley M, Gamble T, Hosseinipour MC, Kumarasamy N, Hakim JG, Kumwenda J, Grinsztejn B, Pilotto JHS, Godbole SV, Mehendale S, Chariyalertsak S, Santos BR, Mayer KH, Hoffman IF, Eshleman SH, Piwowar-Manning E, Wang L, Makhema J, Mills LA, Bruyn GD, Sanne I, Eron J, Gallant J, Havlir D, Swindells S, Ribaudo H, Elharrar, Burns D, Taha TE, Nielsen-Saines K, Celentano D, Essex M, Fleming TR. Prevention of HIV-1 infection with early antiretroviral therapy. N Engl J Med 2011; 365: 493-505.
- Cole SR, Hernan MA, Anastos K, Jamieson BD, Robins JM. Determining the effect of highly active antiretroviral therapy on changes in human immunodeficiency virus type 1 RNA viral load using a marginal structural left-censored mean model. Am J Epidemiol. 2007; 166: 219-227.
- Lecher S, Williams J, Fonjungo PN, Kim AA, Ellenberger D, Zhang G, Toure CA, Agolory S, Appiah-Pippim G, Beard S, Borget MY, Carmona S, Chipungu G, Diallo K, Downer M, Edgil D, Haberman H, Hurlston M, Jadzak S, Kiyaga C, MacLeod W, Makumb B, Muttai H, Mwangi C, Mwangi JW, Mwasekaga M, Naluguza M, NgAngA LW, Nguyen S, Sawadogo S, Sleeman K, Stevens W, Kuritsky J, Hader S, Nkengasong J. Progress with Scale-Up of HIV Viral Load Monitoring ? Seven Sub-Saharan African Countries, January 2015?June 2016. R Morb Mortal Wkly Rep 2016; 65: 1332-1335.
- Chenand B, Zhou XH. Non-homogeneous Markov process models with informative observations with an application to Alzheimer?s disease. Biom J 2011; 53: 444-463.
- Lee S, Ko J, Tan X, patel I, Balakrishnan R, Chang J. Markov Chain Modelling Analysis of HIV/AIDS Progression: A Race Based Forecast in the United States. Indian J Pharm Sci 2014; 76: 107-115
- Lange JM, Hubbard RA, Inoue LYT, Minin V. A joint model for multistate disease processes and random informative observation times, with applications to electronic medical records Data. UW Biostatistics Working Paper Series, 2014: 401.
- Saint-Pierre P, Combescure C, Daures JP, Godard P. The analysis of asthma control under a Markov assumption with use of covariates. Stat Med. 2003; 22: 3755-3770.
- Shoko C, Chikobvu D. Time-homogeneous Markov process for HIV/AIDS progression under a combination treatment therapy: cohort study, South Africa. Theor Biol Med Model 2018; 15: 3.
- Grover G, Gadpayle KA, Swain PK, Deka B. A Multistate Markov Model Based on CD4 cell count for HIV/AIDS Patients on Antiretroviral Therapy (ART). Int J Stat Med Res 2013; 2: 144-151.
- Mathieu E, Foucher Y, Dellamanica P, Daures JP. Parametric and non homogeneous Semi-Markov process for HIV control. Methodol Comput Appl Probab 2007; 9: 389-397.
- Ocarn-Riola R. Non-homogeneous Markov Processes for Biomedical data Analysis. Biom J 2005; 47: 369-376.
- Dessie ZG. Modeling of HIV/AIDS dynamics evolution using non-homogeneous semi-Markov process. SpringerPlus 2014; 3: 537.
- Shoko C and Chikobvu D. Determinants of viral load rebound on HIV/AIDS patients receiving antiretroviral therapy: Results from South Africa. Theor Biol Med Model 2018; 15: 10.
- Shoko C, Chikobvu D. A superiority of viral load over CD4 cell count when predicting mortality in HIV patients on therapy. BMC Infectious Disease. 2019; 19: 169.
- Chikobvu D and Shoko C. A Markov Model to estimate Mortality due to HIV/AIDS using CD4 cell counts based states and viral load: A Principal Component Analysis approach. Biomedical Research. 2018; 29 (15): 3090-3098
- Shoko C, Chikobvu D, Pascal O. Bessong. A Markov Model to estimate Mortality due to HIV/AIDS using viral load levels based states and CD4 cell counts: A Principal Component Analysis approach. Infect Dis Ther 2018; 4: 457-471.
- Jackson C, Multi-state modelling with R: the msm package Version 1.6.4. MRC Biostatistics Unit. 2016
- Silveira MP, De Lourdes DM, Leite JC, Pinheiro CA, Da Silveira VL. Predictors of undetectable plasma viral load in HIV-positive adults receiving antiretroviral therapy in Southern Africa, Braz J Infect Dis 2002; 6: 164-171.
- Azia IN, Mukumbang FC, Van Wyk, B. Barriers to adherence to antiretroviral treatment in a regional hospital in Vredenburg, Western Cape, South Africa. South Afr J HIV Med 2016; 17: 476.


