ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 10
Methodological Comparison of Survival Analysis Methods in Censored Medical Data
1Assoc. Prof., PhD, Department of Biostatistics and Medical Informatics, Faculty of Medicine, Istanbul Aydin University, Turkey
3PhD (Biostatistics), Department of Statistics, Faculty of Science, Ankara University, Ankara, Turkey
4MD, Med. Spec., PhD, Department of History of Medicine and Ethics, Faculty of Medicine, Dokuz Eylul University, Izmir, Turkey
5Division of Developmental Medicine, Boston Children’s Hospital, Harvard Medical School, Boston, Massachusetts, USA
- *Corresponding Author:
- Assoc. Prof. Ayşe Canan Yazıcı Güvercin, PhD
Department of Biostatistics and Medical Informatics
Faculty of Medicine, İstanbul Aydın University
İstanbul, Turkey
Accepted on February 21, 2017
Right censored data is the type of data in which the interested event has not been observed in working period determined initially; or which is arisen in case that any information cannot be taken from a person in the study after a certain period. In this study, it is purposed that survival probabilities of right censored data have been calculated and compared by Kaplan-Meier product limit method (K-M), life table method and exponential and Weibull Distribution methods. The sample has been generated by a simulation basing on data obtained from a research on a chronic illness in a healthcare organization. R Studio software (R Studio Team (2015) has been used in producing dataset. In dataset, there are survival periods and censor states regarding two new treatment methods. The difference between patients’ survival periods has been analysed by according to nonparametric K-M product limit method, semi parametric life table method and parametric exponential and Weibull distribution methods. When methods are compared with each other, nonparametric K-M product limit method estimator informs about the best prediction for current sample. When prediction method is evaluated according to exponential distribution parameters which require parametric assumption, a considerably approximate result to K-M product limit method has been obtained. Using the appropriate statistical analysis method is one of the most fundamental tools for achieving the right information. Physicians making decisions based on accurate information will increase the patient benefit in a medical and ethical way, and will also make a significant contribution to the success of medicine.
Keywords
Survival analysis, Censoring, Kaplan Meier product limit method, Life table, Weibull distribution, Exponential distribution, Beneficence, Medical data.
Introduction
In general, the principle of non-maleficence in medicine is to prevent, reduce and eliminate all kinds of harm [1]. Practices based on inaccurate information obtained through inappropriate statistical analysis methods may harm human health as well as confidence in medicine [2]. Physicians make medical decisions about their own patients based on information such as the patient's medical condition, values, prognosis of the disease, and the effectiveness of the treatment. These decisions are also affecting other patients, since they also include how medical resources are distributed. Survival analysis, which contributes to the process of determining the prognosis of the disease and the effectiveness of the treatment, is a common method of statistical analysis in medicine.
Survival analysis involves advanced methods in order to determine survival probability after a starting point in a certain tracking period until an interested event such as death, illness, and relapse has been occurred, to compare different groups in terms of survival or to examine effects of treatment methods and other factors on survival period [3].
In applied fields, especially clinical studies, it cannot always be possible to observe every person within determined period for the study until interested event has been occurred. Study design containing censoring data has been used in such cases. Because of several limits such as time and cost, censoring is to ignore data which are unknown for certain and cannot be observed for any reason. There are three types of censoring as right censoring, left censoring and interrupted censoring. Right censored data is the type of data in which the interested event has not been observed in working period determined initially after beginning the research; or which is arisen in case that any information cannot be taken from a person in the study after a certain period [4]. It is also known as left censoring if the patient has been on risk for disease for a period before entering the study. Starting point is defined by an event such as entry of patient in trial, randomization or occurrence of a procedure or treatment. Therefore, left censoring is usually not a problem in clinical trials. Time to event may be known only up to a time interval. So, interval censoring occurs in case the assessment of monitoring is done at a periodical frequency [5]. Some methods have been developed for estimating survival function in case of existence of censored data. These are semi parametric such as life table method, nonparametric methods such as K-M product limit method and parametric methods such as Weibull distribution, exponential distribution.
In this study, it is purposed that survival probabilities of right censored data have been calculated and compared by K-M product limit method, life table method and exponential and Weibull distribution methods.
Materials and Methods
In the study, sample size is 264, and the sample has been generated by a simulation basing on data obtained from a research on a chronic illness in a healthcare organization. R Studio software (R Studio Team (2015) has been used in producing dataset [6]. In data set, there are survival periods and censor states regarding two new treatment methods. Two treatment methods and censor states have been generated as dichotomous variables from uniform distribution which is similar to the frequencies and ratios in the baseline study. Survival periods have been also generated from uniform distribution by running to tracking periods of 1, 3, 6, 12, 18, 24, 30, 36, 42 months in accordance with baseline study. The difference between patients’ survival periods has been analysed according to nonparametric K-M product limit method, semi parametric life table method and parametric exponential and Weibull distributions methods. Sample of the study and results of mentioned analysis have been obtained by repeating 100000 times iteratively.
Life table method
Life table method had been developed by Cutler and Ederer (1958). This method is a semi parametric method which evaluates fact results of the study by grouping in the frame of time intervals determined by researcher [7]. Here, death probability is,
qj=λj/(nj-1/2wj) (1)
j: Period of time,
λj: Number of dead patients,
nj: Total number of patients in that time interval,
wj: Number of being withdrawn from observation or being lost while alive.
pj has been calculated by subtracting survival probability, qj in time interval of j, from 1 pj=(1-qj). This probability is a conditional probability; it has been found among people who can live until that time interval.
Kaplan-Meier product limit method
Kaplan-Meier (KM) product limit method is the most common nonparametric method which has been used for censored data developed in consequence of studies on datasets involving uncompleted surviving periods [8]. This method enables to calculate surviving and death functions without dividing data related with survival periods into time intervals [8,9]. The difference of this method from life table method is that tracking period has not been divided into certain time intervals and while death probability is calculated, alive people who are withdrawn from the study is not included to the study again.
In K-M product limit method, survival probability has been obtained by multiplying survival probabilities in every time interval since the beginning of the study [10]. K-M product limit has been obtained as equality (2).
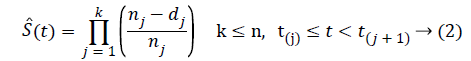
Here,
dj: The number of failures in tj,
nj: Number of individuals at risk in tj,
k: The number of sequential observations,
n: Total number of individuals,
In survival analysis, hazard function is the risk of ending life of a person who stays alive until a certain period (t) in next time interval (Δ+t). Hazard function (h(t)) is also named as failure rate, instantaneous death rate or force of mortality. Hazard function is obtained as equality (3).
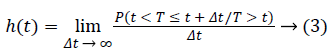
Parametric methods
In survival analysis, data must have a certain distribution for parametric methods to be used. Exponential and Weibull distributions are commonly used as the first survival model. Besides these distributions, distributions such as Gamma, Generalised Gamma and Log-normal have also been used [11]. Maximum likelihood estimator (MLE) is mostly used as parametric method.
Exponential distribution
Although exponential distribution can be statistically applied easily, having constant hazard rate hinders to be suitable model for many conditions. Exponential distribution has only one parameter. This parameter is “constant hazard rate” β. High values are meaning as high risk and short survival, and low β values are meaning low risk and long survival.
Probability density function is like equality (4).
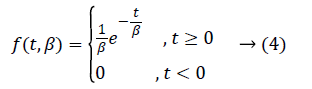
Supposing that in a study in which n number of observations are done, number of d observations are uncensored until the period of t and c=n-d numbers of observations are censored. Here lets censored observations be multiple censored observations. Under the assumption that distribution of right censored data shows exponential distribution, likelihood function of this distribution can be written as equality (5).
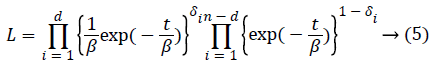
Here, δi=1 has been taken for uncensored observations, and δi=0 has been taken for censored observations. Equality below can be written from equality (5).
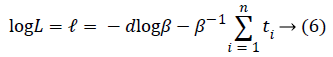
If the first derivative is taken according to β in this expression and is evaluated with zero, MLE of β will be found [12].
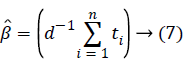
Weibull distribution
It is a two-parameter distribution used in the modelling of the time until a failure occurs or until the second failure occurs after a failure. Weibull distribution is generalised state of exponential distribution. Because it does not have constant hazard rate, its applications are more than exponential distributions. This distribution has been mostly used in reliability and survival studies. Probability density function of Weibull distribution is like equality (8).
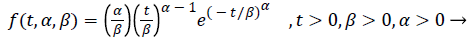 (8)
(8)
Probability density function of Weibull distribution has two parameters such as α (shape) and β (scale). For α=1, the random variable for T has exponential distribution.
To find the most likelihood estimators of unknown μ and σ parameters of this distribution, derivatives of likelihood function have been taken according to α, β and nonlinear equations have been obtained. These equations can be solved within Newton Raphson method.
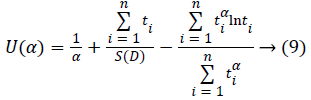
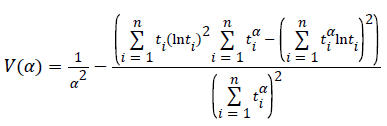
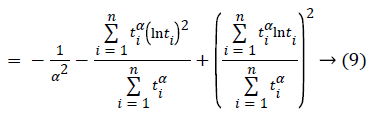
In this case, transaction of iteration has been obtained within α=1 initial value of Newton Raphson method:
If α (m+1) is approximate enough to the number of α (m), α’ (m+1) which is maximum likelihood estimator of α can be found by stopping iteration [13].
Results
Treatment method 1 has been applied to 204 patient and treatment failed in 93 (45.6%) patients and 111 (54.4%) of these are censored data. Similarly, Treatment method 2 has been applied to 60 patients. Treatment failed in 36 (60%) patients and 24 (40.0%) of these are censored data.
Results according to life table method
Life tables of treatment groups has given below Table 1.
| First-order Controls | Number Entering Interval | Number Withdrawing during Interval | Number Exposed to Risk | Number of Terminal Events | Proportion Terminating | Proportion Surviving | Hazard Rate | Std. Error of Hazard Rate | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Treatment | 1,00 | 0 | 204 | 21 | 193,50 | 18 | ,09 | ,91 | ,02 | ,00 |
| 6 | 165 | 3 | 163,50 | 6 | ,04 | ,96 | ,01 | ,00 | ||
| 12 | 156 | 6 | 153,00 | 18 | ,12 | ,88 | ,02 | ,00 | ||
| 18 | 132 | 24 | 120,00 | 18 | ,15 | ,85 | ,03 | ,01 | ||
| 24 | 90 | 18 | 81,00 | 12 | ,15 | ,85 | ,03 | ,01 | ||
| 30 | 60 | 6 | 57,00 | 3 | ,05 | ,95 | ,01 | ,01 | ||
| 36 | 51 | 30 | 36,00 | 12 | ,33 | ,67 | ,07 | ,02 | ||
| 42 | 9 | 3 | 7,50 | 6 | ,80 | ,20 | 0,00 | 0,00 | ||
| 2,00 | 0 | 60 | 3 | 58,50 | 3 | ,05 | ,95 | ,01 | ,01 | |
| 6 | 54 | 0 | 54,00 | 3 | ,06 | ,94 | ,01 | ,01 | ||
| 12 | 51 | 3 | 49,50 | 6 | ,12 | ,88 | ,02 | ,01 | ||
| 18 | 42 | 6 | 39,00 | 6 | ,15 | ,85 | ,03 | ,01 | ||
| 24 | 30 | 0 | 30,00 | 6 | ,20 | ,80 | ,04 | ,02 | ||
| 30 | 24 | 3 | 22,50 | 3 | ,13 | ,87 | ,02 | ,01 | ||
| 36 | 18 | 9 | 13,50 | 9 | ,67 | ,33 | ,17 | ,05 | ||
Table 1. Two groups’ 0-6 months limited 42 month life tables.
The first group’s median survival period is about 36.98 months, and the second group’s mean survival period is calculated as about 32.78 months.
Results according to Kaplan-Meier product limit method
According to Kaplan-Meier product limit method, mean of survival period has been observed as 28.857 ± 2.076 [26.702; 31.012] months in the first treatment method. Survival period mean is 26.062 ± 1.556 [23.013; 29.111] months in the second treatment method.
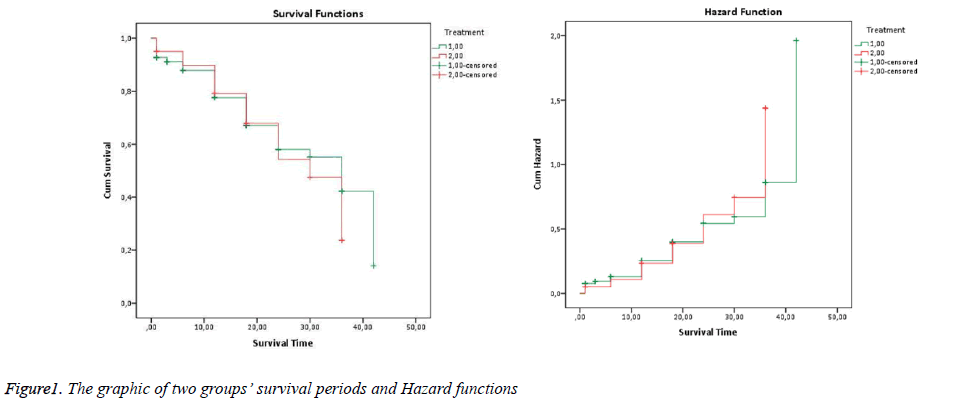
According to results of K-M product limit method estimator, the probability of survival of patients to whom the first treatment method is applied for more than 1 month is 92.6%, probability of survival for more than 3 months is 91%,probability of survival for more than 6 months is 87.7%, probability of survival for more than 12 months is 77.6%, probability of survival for more than 18 months is 67%, probability of survival for more than 24 months is 58.1%, probability of survival for more than 36 months is 42.2%, probability of survival for more than 42 months is 14.1%. Similarly if the table is interpreted for the second treatment method, probability of patients’ survival for more than 1 month is 95%, probability of survival for more than 6 months is 89.7%, probability of survival for more than 12 months is 79.2%, probability of survival for more than 18 months 67.9%, probability of survival for more than 24 months is 54.3%, probability of survival for more than 36 months is 23.8%. It is observed that patients who are observed after 36th month cannot be calculated because they are entirely censored observations.
In the graphic, green lines show the first group’s survival periods, (+) signs show censored observations. Red lines show the second group’s survival periods, (+) signs show censored observations (Figure 1).
Results according to parametric methods
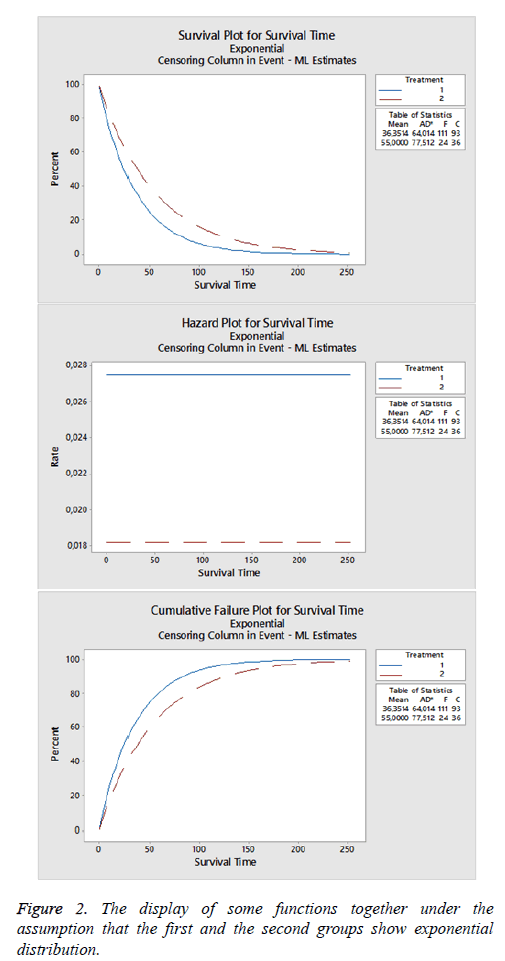
Exponential distribution: In the study, when it is examined under the assumption that dataset is distributed exponentially, it is observed that there are 111 censored 93 failed data for the first group, 24 censored 36 failed data for the second group (Figure 2).
When graphic related with the groups are examined, it can be said that death rate of the second group is lower than the first group and similarly in life functions, the survival probability of the second group is more than the first group. When maximum likelihood estimators are calculated under exponential distribution, mean and standard error are obtained as 36.351 ± 3.450; median value is 25.197 and 95% confidence limits are (20.920; 30.349) for the first group, and mean and standard error are obtained as 55 ± 11.227; median value is 38.123; 95% confidence limits are (25.553; 56.877) for the second group.
Weibull distribution
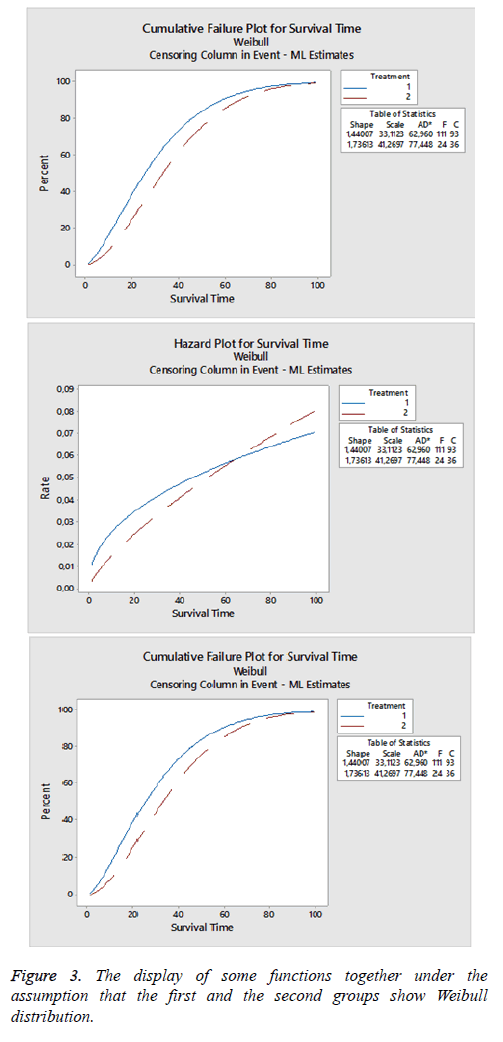
In the study, when it is examined under the assumption that dataset is Weibull distributed, it is observed that that there are 111 censored 93 failed data for the first group, 24 censored 36 failed data for the second group.
The percentage of survival period and failure rate according to time is shown in Figure 3 under the assumption that the first and the second graphics show respectively Weibull distribution. The third graphic gives failure rate. Failure rate for the first group is approximately 0.021, and failure rate for the second group is approximately 0.006.
Estimation values of shape and scale parameters of Weibull distribution are respectively 1.440 and 33.112, standard errors are respectively 0.118 and 2.230; 95% confidence limits are (1.227;1.691) and (29.017;37.785) for the first group. Shape and scale parameter for the second group is estimated 1.736 and 41.270. Standard errors are 0.308 and 5.460; %95 confidence limits are (1.224; 2.458) and (31.843; 53.486).
If we summarize statistics related with estimations of survival period mean according to all the methods that we used in data analyses; mean survival period is estimated as 37 months for the first treatment method and 33 months for the second treatment method according to life table method. According to K-M product limit method, mean survival period of the first treatment method is 28.857 ± 2.076 months, and mean survival period of the second treatment method is 26.062 ± 1.556 months. Parameter value estimated under the assumption that accords with exponential distribution which is one of parametric methods is obtained as 36.351 ± 3.450 for the first group on mean; 55 ± 11.227 for the second group on mean. When patients’ survival periods are observed for Weibull distribution, mean survival period is estimated as 30.052 ± 2.124 and median value is 25.672 days for the first treatment, and mean survival period is estimated as 36.773 ± 5.058 and median value is 33.416 days for the second treatment.
Discussion
In medicine, evaluating results such as mortalities and morbidities that can arise at long term is important. Survival analysis is frequently used in medicine in order to determine death risk of illnesses and prognostic factors on these risks. This analysis has some purposes such as estimating relapse of the illness or person’s life expectancy and determining effectiveness of treatment methods [11]. It is also one of advanced statistical methods for medical applications which contain censored data. There are different approaches related with the solution of interested problem in survival analysis. One of the approaches is to make estimations by using several parametric distributions, and the other is to make estimations by using nonparametric procedures which do not base on any distribution assumptions.
When studies in literature are examined, Tamam et al. analyzed right censored and uncensored data of 137 patients contracting lung cancer and stated that it is suitable to Weibull distribution and he made parametric estimations. They declared that results obtained by using parametric statistical methods give more professional results and therefore they could prefer using important distributions in survival analysis [14]. Dakhil et al. tracked 254 female patients who contracted breast cancer among the years 2005 and 2009 for at least one year and their survival probabilities had been calculated. According to obtained results, a significant difference was found between survival probabilities of patients with malignant and benign tumours [15]. In İnceoğlu’s et al. study, data belonging to 894 patients to whom liver transplant had been applied 10 years period covering 2002-2012 had been used. Patients’ survival periods had been tracked for 27 months after transplantation periods. Dataset had been evaluated within life table analysis, K-M product limit method, Cox regression analysis and their results had been compared. In comparison of factors which affect liver transplantation, they obtained statistically significant results for K-M product limit method and Cox regression analysis methods in one part of variables, and they found significant or insignificant results for per three methods in other part of variables [8].
When life table, K-M product limit, exponential and Weibull methods are compared in this study, nonparametric K-M product limit method estimator gives the best estimation for current sample in iterative evaluation. However, parametric methods have been predicted that there is an increase in survival period. According to results of life table and parametric methods, survival periods approach each other. Approaching semi parametric and parametric methods each other is an expected situation as a consequence of iterative evaluation. It can be said that K-M product limit method estimator, which has no precondition, has not been affected from iteration.
Life table method can be used when survival period is grouped according to intervals and number of death patients in every interval has been calculated. This method also calculates probabilities of censored patients. K-M product limit method is a much-used estimator with regard to be calculated easily, being understandable and estimate only surviving people’s surviving probabilities without calculating censored data. Moreover, nonparametric methods are preferred because they do not require a certain distribution assumption. Estimations of parametric methods are stronger than nonparametric methods. However, if used distribution family complies with examined data, parametric modelling gives better estimations. Any failure in assumptions may lead to bias in estimators obtained as a result of the analyses. Especially existence of censored data may cause problems in examination of suitability of parametric distribution.
Using the appropriate statistical analysis method is one of the most fundamental tools for achieving the right information. Physicians making decisions based on accurate information will increase the patient benefit in a medical and ethical way, and will also make a significant contribution to the success of medicine. In this way, a reliable basis will be reached for physicians to regulate the treatment plans of the patients, and for the patients to decide on their own future.
References
- Beauchamp TL, Childress JF. Principles of Biomedical Ethics, Seventh Edition Oxford University Press, New York 2013.
- Committee on Science, Engineering, and Public Policy, National Academy of Sciences, National Academy of Engineering, and Institute of Medicine. On Being a Scientist: A Guide to Responsible Conduct in Research, The National Academies Press, Washington D.C. 2009.
- Fisher LD, Belle GV. Biostatistics, a methodology for the health sciences, John Wiley & Sons Inc, New York 1993.
- Hosmer DW, Lemeshow S, May S. Applied Survival Analysis: Regression Modeling of Time to Event Data 618. cilt/Wiley Series in Probability and Statistics, John Wiley & Sons Inc, New Jersey 2008.
- Prinja S, Gupta N, Verma R. Censoring in Clinical Trials: Review of Survival Analysis Techniques. Indian J Community Med 2010; 35: 217-221.
- RStudio Team (2015) R Studio: Integrated Development for R. RStudio, Inc, Boston, MA
- Cutler SJ, Ederer F. Maximum Utilization of the Life Table Method in Analyzing Survival. J Chronic Dis. 1958; 8: 699-712.
- Kaplan EL, Meier P. Non parametric estimation from incomplete observations. J Am Stat Assoc 1958; 53: 457-481.
- Özdamar K. SPSS ile Biyoistatistik (in English: Biostatistics with SPSS) (5th Edn) Kaan Kitabevi, Eskişehir 2003.
- Akbar A, Pasha GR. Properties of Kaplan-Meier estimator: group comparison of survival curves. Eur J of Sci Res 2009; 32: 391-397.
- İnceoğlu F. Sağkalım analiz yöntemleri ve karaciğer nakli Verilerine bir uygulama (in English: Survival analysis methods and an application to liver transplantation data). Master's thesis, İnönü University, Institute of Health Sciences, Malatya 2013.
- Schmidt DF, Makalic E. Universal Models for the Exponential Distribution, IEEE Transactions on Information Theory, 2009; 55: 3087-3090.
- Cohen ACJR. Maximum Likelihood Estimation in the Weibull distrubition based on comlete censored samples. Techometrics, 1965; 7: 579-588.
- Tamam D. Tam ve sansürlü örneklem durumlarında Weibull dağılımı için bazı istatistiki sonuç çıkarımları (in English: Some statistical conclusion inferences for Weibull distribution in complete and censored sample cases). Master's thesis, Ankara University, Institute of Science, Ankara 2008.
- Dakhil NK, Al-Decemberali YM, Al-A’bidy MAM. Analysis of breast cancer data using Kaplan-Meier analysis. Journal of Kufa for Mathematics and Computer, 2012; 1: 7-14.