ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2018) Volume 29, Issue 12
Finite element approach towards impact analysis on biomechanical nature of cornea
Dibyendu Mandal*, Himadri Chattopadhyay, Amit Karmakar and Kumaresh Halder
Department of Mechanical Engineering, Heat and Power Laboratory, Jadavpur University, Kolkata, India
- *Corresponding Author:
- Dibyendu Mandal
Department of Mechanical Engineering
Heat and Power Laboratory
Jadavpur University, India
Accepted on May 11, 2017
DOI: 10.4066/biomedicalresearch.29-16-1650
Visit for more related articles at Biomedical ResearchThe present work is a computational analysis of a blunt body impact on corneal viscoelastic behavior; simultaneously comparison is drawn between the tissue behaviors with corresponding cases considering the tissue to be elastic in other simulated model. Three dimensional models of corneal tissue were subjected to blunt body impact at different velocities in ALTAIR platform to study the nature of injury on the tissue material. The variation in the strain due to impact on the cornea for the material behaviors, range in the order 10-2 ± 0.002 and that for the stress, the magnitude gets almost double for elastic nature of cornea. Results shows that the viscoelastic fractional derivative biomechanics of the tissue predict higher resistance to any foreign body impacting on the surface of cornea preventing it from further indentation into the tissue. The viscoelastic model provided in this work can be incorporated for the synthesis of artificial corneas and soft contact lenses.
Keywords
Cornea, Fractional kelvin voigt model, Biomechanical properties, Viscoelasticity, Finite element simulation.
Introduction
Ocular injury can lead to extensive tissue damage which results in ocular emergency situations and serious morbidity of the delicate tissues of the eye [1]. Injuries due to larger impacting bodies cause wear and tear of the eye lid tissues, retinal detachment from choroid or equatorial expansion of the eye ball. But injury due to small foreign body can also lead to the injuries direct on the surface of cornea, which may lead to complete or partial tissue rupture leading to complete loss of vision or impaired vision. Eye is one of the major sense organ of our body. It has three membrane layers, sclera, choroid and retina from outer layer to inner layer that surrounds the eye. The sclera continues in front of the eye ball as a transparent layer named cornea which helps in reflection of the light into the eye and also protect the inner parts and tissues of the eye. Thus cornea is a part of major clinical and medical concern. Recently researchers are focusing on the biomechanical characteristics of the morbid eye tissues where increase in intraocular pressure (IOP) results in increase of stress which is a characteristic of the deformation of cornea [2]. To properly understand the process of these ocular diseases a better visualization and understanding of the mechanical nature of the corneal tissue is of prior importance. The main objective of this work is to focus on the material characteristics behavior of synthetic cornea or contact lenses which is subjected to regular impact. A three dimensional Finite Element Analysis (FEA) is applied for understanding and analyzing the impact of foreign body causing Intra-Ocular Foreign Body (IOFB) injuries. Blunt eye trauma comprises injuries to the closed globe where tissue damage can results from mechanical deformation alone or combined effect of direct delivery of energy to the tissue due to impact [3]. A particular tissue’s behavior and deformation under stress is determined by its biomechanical properties.
Finite Element Modeling (FEM) is a numerical analytical approach, extensively used for simulation of multiphysics problems that involves complex structures and loading conditions [4]. This method, since past few years, is applied to biological systems, specifically to the eye for simulation of the stress-strain nature of the lamina cribrosa layer, the corneal tissue and the whole eye [5-7]. A simulation model of eye is set up based on the information of cadaver eyes done in the earlier works in this domain. The scope of the present work is to investigate an FEM analysis of a standardized corneal trauma due to blunt body impact where the tissue is considered to be viscoelastic in nature, and to draw a comparison between the tissue behaviors with corresponding cases considering elastic behavior only.
Materials and Methods
Cornea exhibits unique properties of stiffness, mechanical strength and optical transparency which enable it to provide protective barrier to the inner components of the globe and also the primary refractive medium of the eye. The fibrous microstructure of the stromal layer of cornea, which in humans constitutes 90% of the corneal thickness, results in this unique nature of the tissue. The stromal thickness is composed of around 200 lamellar sheets of collagen myofibrils implanted in hydrated matrix of glycoproteins, keratocyte cells and proteoglycans [8]. Cornea exhibits complex microstructure strongly regulated by the human body itself. After death, the cornea swells and its optical clarity and tear film is lost. Thus the biomechanical properties of the eye changes due to the combined effect of these biomechanical changes along with tissue degradation and alteration in temperatures [9]. In addition, Kobayashi et al. explained that the cornea is not purely elastic but rather is viscoelastic, which means the loading rate applied on the tissue alters the calculated value of the Young modulus [10]. Due to the combination of all these factors, previous literatures has reported large range of Young’s Modulus ranging from 0.159 MPa to 57 MPa [11,12]. Under loading condition, cornea shows instantaneous deformation which demonstrates purely elastic response followed by gradual and progressive deformation which signifies its viscoelastic nature [10,13]. These behaviors could be modeled fairly with a Hookian spring system for pure elastic nature and with a spring-dashpot system for the viscoelastic nature, where the dashpot represents time-dependent viscous resistance to an applied force. Here one spring-mass system is in series with a spring-mass damping system where the damping is parallel to the spring system.
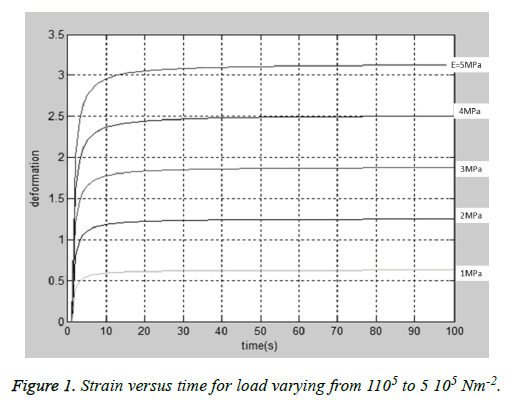
For viscoelastic model, generalized Fractional Kelvin-Voigt Deravativehas been selected as other model (e.g. Maxwell model) continually to creeps indefinitely under load. In the cornea, creep approaches asymptotically [14]. Another limitation of Maxwell model is that it does not regain its original form after the load cease to act. The pure Kelvin-Voigt model was not selected because it does not possess a purely elastic component and thus no instantaneous deformation occurs. A simple graphical model has been developed in MATLAB for a corneal model with Young’s modulus in the above mentioned range and viscosity of 9.02 KPa-s, which shows time-dependency of the deformation for a particular load. Figure 1 shows that the steepness of the curve increases as the stress increases and after the elastic limit it experiences no further deformation.
The elastic nature of the model is assumed to be an isotropic, linear elastic model obeying Hook’s law and represents a linear relation between stress and strain. The stress-strain relationship could be presented as:
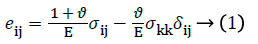
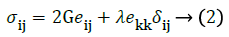
Where, eij represents the Eulerian strain tensor and σij represents Cauchy stress tensor’s component [15].
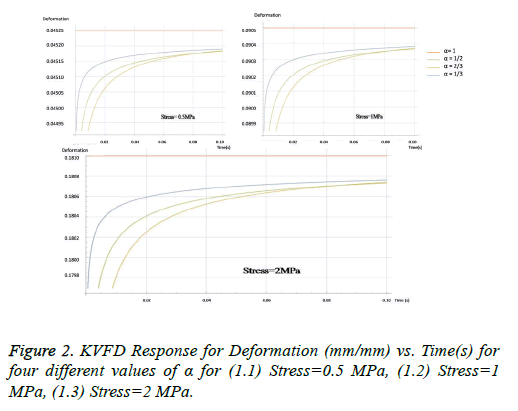
KVFD governing equation 4 arises out of the conventional governing equation 3 of the K-V Model by replacing the ordinary integral derivatives with a fractional order. Order of the derivative of strain with respect to time is thus assumed to be a fraction and the corresponding stress-strain plot has been obtained. Stress has been varied between 1 MPa-9 MPa and the corneal tissue has a co-efficient of viscosity of 9.02 KPa and elastic limit of 11.05 MPa [16-18]. These data have been incorporated into the governing equation of KVFD to obtain the characteristic plots. The fractional order α takes up values such as 1/3, 2/3, 1/2, 1/4 and 3/4. When α=1, KVFD reduces to the conventional K-V Model.
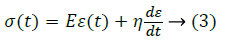
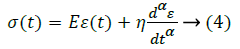
Stress relaxation and Creep Compliance response for a KVFD model are obtained by taking a Heaviside function of the deformation and stress respectively. In the standard Kelvin- Voight model α=1, and the stress relaxation is equal to a delta function at time zero with a constant response after. No real material follows this function. In the KVFD model, where 0<α<1 the stress relaxation has the form t-α, where t is time. The creep compliance, J(t), and stress relaxation, G(t), functions, for the KVFD model are [19]:
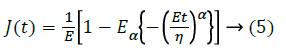
Where, Eα is the Mittag-Leffler function and is given by:
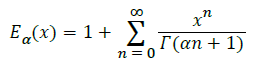
And,
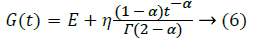
Figure 2 shows that KVFD depicts predicted nature of plot for deformation against time, where the deformation is increasing exponentially in the beginning and then converges within a very short interval of time for various α values: 1/3, 2/3, ½ and 1.
Nguyen et al. suggested the development of a constitutive model based on the tissue microstructure for the nonlinear anisotropic viscoelastic tensile behavior of the stroma layer that comprise a explanation of fully nonlinear viscoelastic response of the lamellar level [20]. The model is based on a newly developed general nonlinear constitutive framework for soft fiber-reinforced composites [21]. The model represents the stroma as a continuum mixture consisting of collagen fibrils structured into lamellae characterized by an in plane orientation angle and embedded in a soft isotropic matrix.
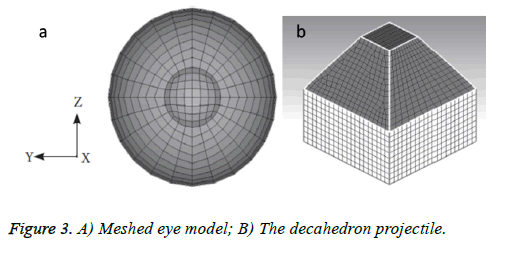
The geometric model for the present work is based on the size, structure and dimensions of a generic human eye model. The model has been derived from our previous work which is a three-dimensional geometry of eye cornea that has been developed and imported in Altair Hyperworks 10.0 suite in Block 90 format and linear hexahedral volume mesh is generated throughout the thickness of the cornea and is constituted of eight nodes hexahedral element called hex8 element in Altair Hypermesh environment, containing total 3095 elements comprising off 3960 nodes shown in Figure 3a [22].
From the experiment report of Uchio et al. it was found that Poisson’s ratio for cornea is 0.420 and it was assumed that rupture occurs at a strain of 18% in cornea, and at a stress of 9.4 MPa [23]. The blunt decahedron projectile, shown in Figure 3b, is generated based on previous work of Uchio et al. and Mousavi et al. [23,24]. Three different materials were considered for projectile i.e., aluminum, bone and stainless steel with corresponding material properties. The bullet projectile has been meshed with linear hexahedral brick element mesh comprising of total 980 elements with 1124 nodes.
The mechanical properties used for various materials are enumerated in Table 1 [25,26]. The base area of the projectile is 0.25 mm2 whose mass varies depending on the material. The cornea geometry is constrained about all axes to prevent any linear or rotational movement in any directions and the projectile material is set to impact on the surface at variable speed of 25 ms-1, 50 ms-1, 75 ms-1 and 100 ms-1. The computation has been performed in Z230 HP workstation.
| Material | Density (gm/cm3) | Young’s Modulus (Mpa) | Poisson’s Ratio |
|---|---|---|---|
| Bone | 1.9 | 9000 | 0.30 |
| Aluminium | 2.7 | 69000 | 0.35 |
| Steel | 3.0 | 197000 | 0.29 |
Table 1. Mechanical properties of various materials considered to be as the foreign body.
Result and Discussions
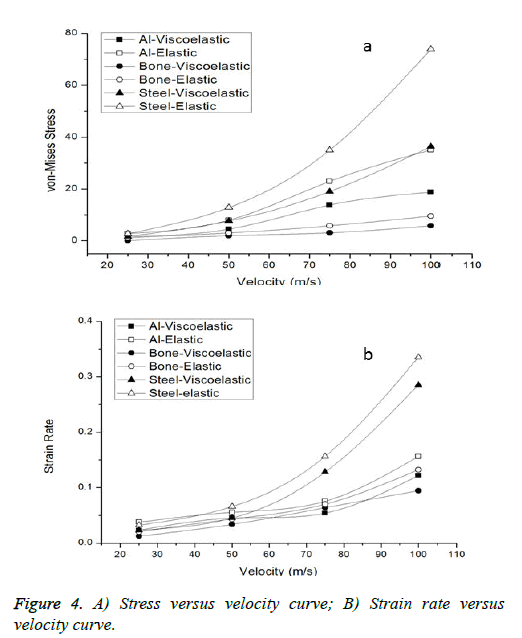
It has been observed through the simulation result that when the corneal tissue is considered as viscoelastic in nature it offers better resistance to the impacting object. The magnitude of the von-Misses stress generated on the surface of the elastic nature cornea almost gets double compared to the viscoelastic nature of the tissue. In the case of strain rate it has been observed that the localized straining is more on the surface of the elastic tissue. The variation in the strain effect on the cornea surface for both the material behavior range in the order 10-2 ± 0.002. It is mainly observed how the strain behavior and von Misses stress behavior varies on the surface of the cornea when crashed with projectiles of such varied mechanical properties. Human cortical bone has the lowest range of Young’s modulus and density among the three materials used, the other two being Aluminum and stainless steel of grade AISI 316. The results are plotted for both plastic strains and Von Misses stresses of the cornea for all the three impacting material and for both the mechanical nature of cornea. From the plots it could be easily said that the value of the result parameters increases with increase in velocities. The plots also depicts that the value of both the result parameters sharply varies with the mechanical properties of the impacting material used for given set of velocities as shown in Figures 4a and 4b.
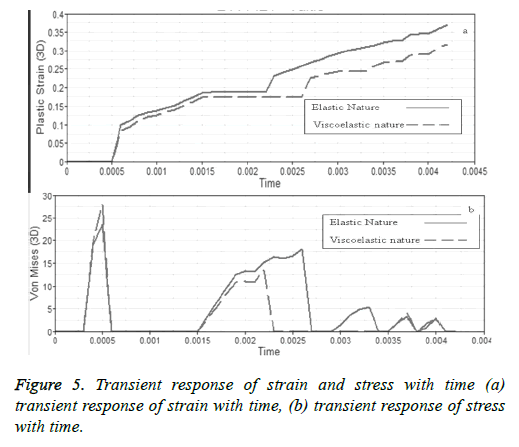
The higher the Young’s Modulus and density of the material higher is the value of plastic strain and von Misses stress at a particular velocity. Stress and strain are generated and transient behavior plot of the strain and stress on the tissue surface are developed which is shown in Figure 5 for the case of an aluminum projectile with a velocity of 50 ms-1. From the transient response of the stress and strain, it is observed that the stress generated and strain effect on the tissue surface due to high velocity blunt body impact is comparably less for the viscoelastic nature of cornea than that of the elastic nature for similar test conditions. This leads to better energy absorption in the model constituted with viscoelastic nature thus it could provide better and long term resistance to the impacting body before failure.
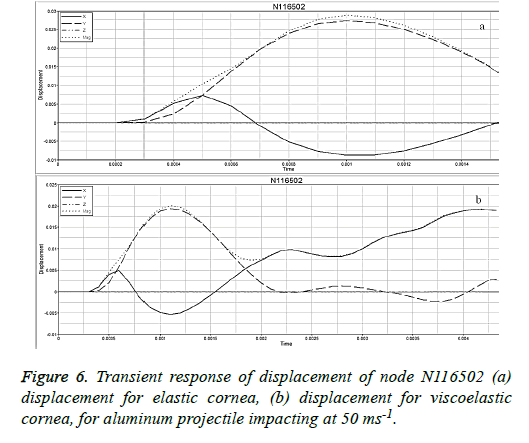
In this study the displacement of the surface of the cornea is also studied. The transient response of the displacement is shown in Figure 6 where it is clearly explained that elastic nature shows instantaneous deformation and is short termed but viscoelastic nature shows prolonged and progressive deformation. Table 2 shows the duration of deformation for different material and projectile velocity combination. There in all the cases we can observe that for viscoelastic model the deformation is much gradual than the elastic model. In our range of maximum velocities, it has been observed that maximum duration for energy absorption is around 5.0, 5.5 and 6.5 milli-second respectively for each of the projectile material. However, the transient response time increases as the elastic moduli and density of the projectile increases. For example the duration of deformation for bone projectile impact is about 5.0 milli-seconds whereas for that of steel is around 6.5 millisecond.
| Velocities (ms-1) | 25 | 50 | 75 | 100 | Projectile Material | ||||
|---|---|---|---|---|---|---|---|---|---|
| Duration of Deformation (sec) | E | VE | E | VE | E | VE | E | VE | |
| 0.0007 | 0.0028 | 0.0010 | 0.0037 | 0.0016 | 0.0045 | 0.0021 | 0.0051 | Bone | |
| 0.0011 | 0.0035 | 0.0015 | 0.0043 | 0.0019 | 0.0051 | 0.0025 | 0.0056 | Aluminum | |
| 0.0016 | 0.0043 | 0.0022 | 0.0052 | 0.0026 | 0.0059 | 0.0031 | 0.0066 | Steel | |
Table 2. Duration of deformation for different cornea material behavior and projectile velocity combination; E: Elastic model of cornea, VE: Viscoelastic model of cornea.
Due to this prolonged deformation stage in viscoelastic model which is not an instantaneous shock to the material rather it follows a gradual deformation with respect to the force applied, this model could be used for further research in this area. Cadaver eye cornea transplant reported several issues of donor graft rejection, biocompatibility and such other issues and antirejection drugs are commonly administered which could lead to infections [27]. The Generalised Kelvin-Voigt Model that has been used in this study could provide a better alternative for donor cadaver cornea as this model with conjunction to the silica composite synthetic cornea can provide a far better viscoelastic barrier similar to collagen tissues. This behavior of material properties could also be used in artificial soft contact lenses to resist any damage to the prosthesis from crash injuries or environmental hazards.
Acknowledgment
We would like to acknowledge the Altair India Support Team for their constant technical support during the research. I like to acknowledge JRF Fellowship of UGC, Government of India for financial support.
References
- Vajpayee RB, Shekhar H, Sharma N, Jhanji V. Demographic and clinical profile of ocular chemical injuries in the pediatric age group. Ophthalmology 2014; 121: 377-380.
- Glass DH, Roberts CJ, Litsky AS, Weber PA. A Viscoelastic Biomechanical Model of the Cornea Describing the Effect of Viscosity and Elasticity on Hysteresis. Invest Ophthalmol Vis Sci 2008; 49: 3919-3926.
- Kuhn F, Morris R, Whiterspoon CD, Heimann K. A standardized classification of ocular trauma terminology. Ophthalmology 1996; 103: 240-243.
- Rossi T, Boccassini B, Esposito L. The Pathogenesis of Retinal Damage in Blunt eye Trauma: Finite Element Modeling. Invest Ophthalmol Vis Sci 2011; 52: 3994-4002.
- Roberts MD, Liang Y, Sigal IA. Correlation between local stress and strain and lamina cribrosa connective tissue volume fraction in normal monkey eyes. Invest Ophthalmol Vis Sci 2010; 51: 295-307.
- Gefen A, Shalom R, Elad D, Mandel Y. Biomechanical analysis of the keratoconic cornea. J Mech Behav Biomed Mater 2009; 2: 224-236.
- Amini R, Barocas VH. Anterior chamber angle opening during corneo-scleral indentation: the mechanism of whole eye globe deformation and the importance of the limbus. Invest Ophthalmol Vis Sci 2009; 50: 5288-5294.
- Maurice DM. The structure and transparency of the cornea. J Physiol 1957; 136: 263-286.
- Hjortdal JO. Extensibility of the normo-hydrated human cornea. Acta Ophthalmol Scand 1995; 73: 12-17.
- Kobayashi AS, Staberg LG, Schelge WA. Viscoelastic properties of human cornea. Exp Mech 1973; 497-503.
- Elsheikh A, Wang D, Brown M, Rama P, Campanelli M, Pye D. Assessment of corneal biomechanical properties and their variation with age. Curr Eye Res 2007; 32: 11-19.
- Andreassen TT, Simonsen AH, Oxlund H. Biomechanical properties of keratoconus and normal corneas. Exp Eye Res 1980; 31: 435-441.
- Edmund C. Corneal topography and elasticity in normal and keratoconic eyes. A methodological study concerning the pathogenesis of keratoconus. Acta Ophthalmol Suppl 1989; 193: 1-36.
- Jue B, Maurice DM. The mechanical properties of the rabbit and human cornea. J Biomech 1986; 19: 847-853.
- Material Laws. Large Displacement Finite element analysis-Part2. RADIOSS Theory Manual v10.0, 2009.
- Uchio E, Watanabe Y, Kadonosono K, Matsuoka Y, Goto S. Simulation of airbag impact on eyes after photorefractive keratectomy by finite element analysis method. Graefe’s Arch Clin Exp Ophthalmol 2003; 241: 497-504.
- Glass DH, Roberts CJ, Litsky AS, Weber PA. A Viscoelastic Biomechanical Model of the Cornea Describing the Effect of Viscosity and Elasticity on Hysteresis. Invest Ophthalmol Vis Sci 2008; 49: 3919-3926.
- Wua J, Nasseri MA, Eder M, Gavaldon MA, Lohmann CP, Knoll A. The 3D Eyeball FEA Model with Needle Rotation. APCBEE Procedia 2013; 7: 4-10.
- Lawrence ST, Amy LL, Deborah JR, Kevin JP. A Kelvin-Voigt Fractional Derivative Model for Viscoelastic Characterization of Liver Tissue. ASME Int Mech Engg Congress and Exposition 2002.
- Nguyen TD, Jones RE, Boyce BL. A Nonlinear Anisotropic Viscoelastic Model for the Tensile Behavior of Corneal Stroma. J Biomech Eng 2008; 130: 1-10.
- Nguyen TD, Jones RE, Boyce BL. Modelling the Anisotropic Finite-Deformation Viscoelastic Behavior of Soft Fiber-Reinforced Composites. Int J Solids Struct 2007; 44: 8366-8389.
- Mandal D. Simulation of eye Injury due to blunt body impact. DSpace of Jadavpur University 2013; Kolkata, India.
- Uchio E1 Ohno S, Kudoh J, Aoki K, Kisielewicz LT. Simulation model of an eyeball based on finite element analysis on a supercomputer. Br J Ophthalmol 1999; 83: 1106-1111.
- Mousavi SJ, Nassiri N, Masoumi N, Nassiri N, Majdi-N M, Farzaneh S, Djalilian AR, Peyman GA. Finite element analysis of blunt foreign body impact on the cornea after PRK and LASIK. J Refract Surg 2012; 28: 59-64.
- Rupin F, Amena S, Dolmas D. Experimental determination of Young’s Modulus and Poisson ratio in cortical bone tissue using high resolution Scanning Acoustic Microscopy and Nanoindentation. J Acoustic Soc Am 2008; 123: 3785-3795.
- Geringer J, Atmani F, Forest B. Friction Corrosion of AISI 316L/Bone Cement and AISI 316L/PMMA contacts: ionic strength on tribological behavior. Wear 2008; 267: 763-769.
- http://webeye.ophth.uiowa.edu/eyeforum/tutorials/Cornea-Transplant-Intro/index.htm